边心距
正多边形的边心距是正多边形的外接圆圆心(同时也是内切圆圆心)到正多边形某一边的距离。正多边形的边心距都相等,并等于其内切圆的半径。
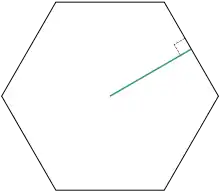
正六边形的边心距
边心距的性质
如果用a表示边心距,s表示边长,p表示多边形的周长,正多边形的面积可以分割成n个小三角形求和,最终结果表示为:
其内切圆的面积可以表示为:
做出边心距和计算
已知正多边形中心的情况下,边心距可通过从正多边形中心向某一边作垂线段;或连接正多边形中心和某一边的中点求得。不知中心的情况下,可以根据垂径定理,通过两条边的垂直平分线的交点来确定正多边形的中心,然后求出边心距。
边心距可以通过正多边形外接圆的半径和边长求出,如果正n边形的外切圆的半径为R边长为s,则边心距为:
外部链接与参考文献
- Apothem of a regular polygon With interactive animation
- Apothem of pyramid or truncated pyramid (页面存档备份,存于)
- Sagitta, Apothem, and Chord (页面存档备份,存于)
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.