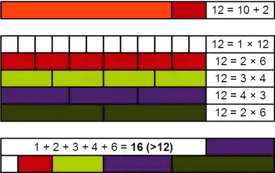
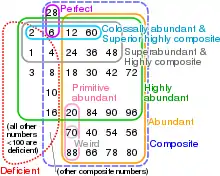
过剩数
定義
一般定义
一般而言,過剩數是指使得函数 的正整数 ,其中 指的是 的真因數之和; 称作 的盈度或豐度。
严格定义
更为严格地说,過剩數是指使得函数 的正整数 ,其中 指的是 的所有正因数(包括 )之和; 称作 的盈度或豐度。
在这种定义下,12的正因數有1、 2、 3、 4、 6和12,由于 ,且 ,因此12為過剩數,且12的豐度為 。
性質
- 945、 1575、 2205、 2835、 3465、 4095、 4725、 5355、 5775、 5985、 6435、 6615、 6825、 7245、 7425、 7875 ……
- 不能被2和3整除的最小過剩數是 5391411025,其質因數有 5、 7、 11、 13、 17、 19、 23 和 29(OEIS數列A047802)。
- 亞努奇(Iannucci)在2005年給出了一個尋找不能被前個質數整除的最小過剩數的演算法[1]:若 表示不能被前 個質數整除的最小過剩數,則當 足夠大時,對所有的 ,有
- 除了完全數本身,完全數的倍數都是過剩數[3]。例如,每個大於6之6的倍數都是過剩數,因為 。
- 過剩數的倍數都是過剩數[3]。例如,20是過剩數,20及其倍數也都是過剩數,因為 。
- 由於完全數的倍數都是過剩數,過剩數的倍數也都是過剩數[3],因此奇數和偶數的過剩數都有無限多個。
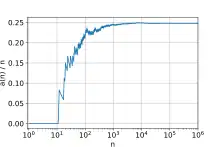
在的分布情況(對數尺度)。其中為不超過的過剩數個數。
相關概念
參考文獻
- D. Iannucci, , Bulletin of the Belgian Mathematical Society, 2005, 12 (1): 39–44 [2022-09-21], (原始内容存档于2019-04-07)
- Tattersall, James J. 2nd. Cambridge University Press. 2005. ISBN 978-0-521-85014-8. Zbl 1071.11002.
- Tattersall (2005)[2], p.134
- Hall, Richard R.; Tenenbaum, Gérald. . Cambridge Tracts in Mathematics 90. Cambridge: Cambridge University Press. 1988: 95. ISBN 978-0-521-34056-4. Zbl 0653.10001.
- Deléglise, Marc. . Experimental Mathematics. 1998, 7 (2): 137–143 [2022-09-21]. CiteSeerX 10.1.1.36.8272
 . ISSN 1058-6458. MR 1677091. Zbl 0923.11127. doi:10.1080/10586458.1998.10504363. (原始内容存档于2020-10-13).
. ISSN 1058-6458. MR 1677091. Zbl 0923.11127. doi:10.1080/10586458.1998.10504363. (原始内容存档于2020-10-13). - Weisstein, Eric W. (编). . at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- Erdős adopts a wider definition that requires a primitive abundant number to be not deficient, but not necessarily abundant (Erdős, Surányi and Guiduli. Topics in the Theory of Numbers p214. Springer 2003.). The Erdős definition allows perfect numbers to be primitive abundant numbers too.
- Sloane, N.J.A. (编). . The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- Benkoski, Stan. . The American Mathematical Monthly. Aug.-September 1972, 79 (7): 774. doi:10.2307/2316276.
- Hagis, Peter; Cohen, Graeme L. . J. Austral. Math. Soc. Ser. A. 1982, 33 (2): 275–286. MR 0668448. doi:10.1017/S1446788700018401.
- Laatsch, Richard. . Mathematics Magazine. 1986, 59 (2): 84–92. ISSN 0025-570X. JSTOR 2690424. MR 0835144. Zbl 0601.10003. doi:10.2307/2690424.
- Sloane, N.J.A. (编). . The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- Sloane, N.J.A. (编). . The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.