長球面坐標系
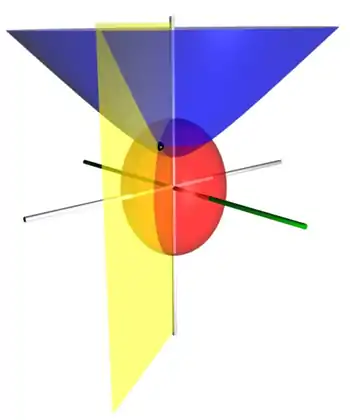
長球面坐標系(英語:)是一種三維正交坐標系。設定二維橢圓坐標系包含於 xz-平面;兩個焦點 與 的直角坐標分別為 與 。將橢圓坐標系繞著 z-軸旋轉,則可以得到長球面坐標系。(假若,繞著 y-軸旋轉,則可以得到扁球面坐標系。)橢圓坐標系的兩個焦點,包含於 z-軸。長球面坐標系可以被視為橢球坐標系的極限案例,其兩個最短的半軸的長度相同。
基本定義
在三維空間裏,一個點 P 的長球面坐標 常見的定義是
- 、
- 、
- ;
其中, 是個實數,弧度 ,弧度 。
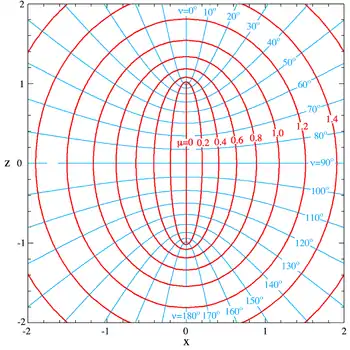
坐標曲面
- 。
每一個長球面都是由橢圓繞著 z-軸旋轉形成的。橢球面與 xz-平面的相交,是一個橢圓。沿著 x-軸,橢圓的短半軸長度為 ,沿著 z-軸,橢圓的長半軸長度為 。橢圓的焦點都包含於 z-軸,z-坐標分別為 。
坐標曲面是半個旋轉雙葉雙曲面:
- 。
當 時,坐標曲面在 xy-平面以上;當 時,坐標曲面在 xy-平面以下。
坐標曲面是個半平面 :
- 。
第二種表述
另外,還有一種比較有幾何直覺性的扁球面坐標系 :
- 、
- 、
- 。
其中, 是個實數, 是個實數,弧度 。
與扁球面坐標系不同,長球面坐標系並沒有簡併。在三維空間裏,長球面坐標系與直角坐標有一一對應關係:
- 、
- 、
- 。
坐標曲面
- 。
每一個長球面都是由橢圓繞著 z-軸旋轉形成的。橢球面與 xz-平面的相交,是一個橢圓。沿著 x-軸,橢圓的短半軸長度為 ,沿著 z-軸,橢圓的長半軸長度為 。橢圓的焦點都包含於 z-軸,z-坐標分別為 。
坐標曲面是半個旋轉雙曲面:
- 。
當 時,坐標曲面在 xy-平面以上;當 時,坐標曲面在 xy-平面以下。
坐標曲面是個半平面 :
- 。
任何一點 P 與焦點 , 的距離 , ,可以一個很簡單的公式表示:
- 、
- 。
所以,點 P 與焦點 的距離 是 ,點 P 與焦點 的距離 是 。(回想 , 都是在 z-軸,分別位於 , 。)
參閱
參考目錄
不按照命名常規
- Morse PM, Feshbach H. . New York: McGraw-Hill. 1953: p. 661. 採用 、 、 。
- Zwillinger D. . Boston, MA: Jones and Bartlett. 1992: p. 114. ISBN 0-86720-293-9. 如同 Morse & Feshbach (1953) ,採用 來替代 。
- Smythe, WR. 3rd ed. New York: McGraw-Hill. 1968.
- Sauer R, Szabó I. . New York: Springer Verlag. 1967: p. 97. 採用混合坐標 、 、 。
按照命名常規
- Korn GA, Korn TM. . New York: McGraw-Hill. 1961: p. 177. 採用第一種表述 ,又加介紹了簡併的第三種表述 。
- Margenau H, Murphy GM. . New York: D. van Nostrand. 1956: p. 180–182. 如同 Korn and Korn (1961) ,但採用餘緯度 來替代緯度 。
- Moon PH, Spencer DE. . corrected 2nd ed., 3rd print ed. New York: Springer Verlag. 1988: pp. 28–30 (Table 1.06). ISBN 0-387-02732-7. Moon and Spencer 採用餘緯度常規 ,又改名 為 。
特異命名常規
- Landau LD, Lifshitz EM, Pitaevskii LP. 2nd edition. New York: Pergamon Press. 1984: pp. 19–29. ISBN 978-0750626347. 視長球面坐標系為橢球坐標系的極限。