阿多米安分解法

阿多米安分解法（Adomian decomposition method，简称：ADM法），是1989年美国籍阿马尼亚数学家George Adomian创建的近似分解法，用以求解非线性偏微分方程[1][2]

将非线性偏微分方程写成如下形式：

$L(u)+R(u)+NL(u)=g(x,t)$

其中 L、R为线性偏微分算子，NL为非线性项。将反算子 $L^{-1}=\int _{0}^{t}()$ . 用于上式

$L^{-1}L(u)=-L^{-1}R(u)-L^{-1}NL(u)+L^{-1}g(x,t)=$ .

得

$u(x,t)=u(x,0)-L^{-1}NL(u)+L^{-1}g(x,t)$ .

令方程的解u（x,t) 为：

u=u_{0}+u_{1}+u_{2}+u_{3}+\cdots

非线性项

NL（u）= $A_{0}+A_{1}+A_{2}+\cdots$

其中

A_{n}={\frac {1}{n!}}{\frac {\mathrm {d} ^{n}}{\mathrm {d} \lambda ^{n}}}f(u(\lambda ))\mid _{\lambda =0},

${\frac {\mathrm {d} ^{n}}{\mathrm {d} \lambda ^{n}}}u(\lambda )\mid _{\lambda =0}=n!u_{n}$

由此得

u(x,t)=u(x,0)+L_{-1}g(x,t)

u_{1}(x,t)=-L^{-1}Ru_{0}-L^{-1}A_{0}

u_{n}(x,t)=-L^{-1}Ru_{n-1}-L^{-1}A_{n-1}

近似解= $u_{0}(x,t)+u_{1}(x,t)+u_{2}(x,t)+u_{3}(x,t)+\cdots$

Burgers-Fisher 方程 ADM解

Burgers-Fisher方程：

{\frac {\partial u}{\partial t}}+u^{2}*{\frac {\partial u}{\partial x}}-{\frac {\partial ^{2}u}{\partial u^{2}}}=u*(1-u^{2})

u[0]=tanh(x)

u[1]=-tanh(x)*(1-tanh(x)^{2})*t

u[2]=-(1/2)*t^{2}*tanh(x)*(-1+tanh(x)^{2})*(2-4*tanh(x)^{2})

u[3]=-(1/3)*t^{3}*tanh(x)*(3-16*tanh(x)^{2}+26*tanh(x)^{4}-13*tanh(x)^{6}-3*tanh(x)^{2}*(1-tanh(x)^{2})+(2*(1-tanh(x)^{2}))*tanh(x)^{4})

近似解：

pa := (-1.*tanh(x)-82360.*tanh(x)^13+73.*tanh(x)^3-1195.*tanh(x)^5+8233.*tanh(x)^7-29990.*tanh(x)^9+63510.*tanh(x)^15-26980.*tanh(x)^17+4862.*tanh(x)^19+63850.*tanh(x)^11)*t^9+(14650.*tanh(x)^13-16170.*tanh(x)^11+tanh(x)+1430.*tanh(x)^17+688.8*tanh(x)^5+10230.*tanh(x)^9-7102.*tanh(x)^15-54.67*tanh(x)^3-3672.*tanh(x)^7)*t^8+(-373.8*tanh(x)^5+1491.*tanh(x)^7-1.*tanh(x)+39.67*tanh(x)^3+3333.*tanh(x)^11+429.*tanh(x)^15-3036.*tanh(x)^9-1881.*tanh(x)^13)*t^7+(132.*tanh(x)^13+187.8*tanh(x)^5-502.*tanh(x)^11+743.5*tanh(x)^9-27.67*tanh(x)^3+tanh(x)-534.6*tanh(x)^7)*t^6+(-135.3*tanh(x)^9+161.1*tanh(x)^7-1.*tanh(x)+42.*tanh(x)^11-85.13*tanh(x)^5+18.33*tanh(x)^3)*t^5+(-37.*tanh(x)^7+33.33*tanh(x)^5+14.*tanh(x)^9-11.33*tanh(x)^3+tanh(x))*t^4+(5.*tanh(x)^7-10.33*tanh(x)^5+6.333*tanh(x)^3-1.*tanh(x))*t^3+(-3.*tanh(x)^3+tanh(x)+2.*tanh(x)^5)*t^2+(-1.*tanh(x)+tanh(x)^3)*t+tanh(x)

迪姆方程ADM解

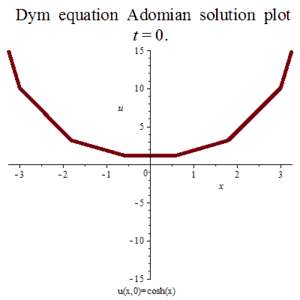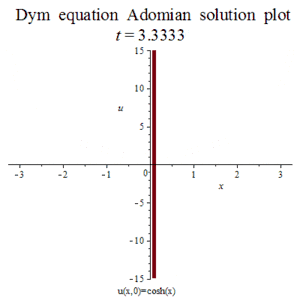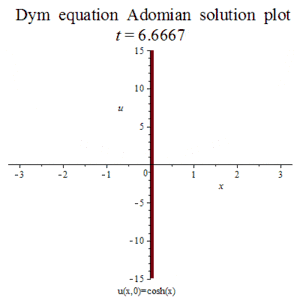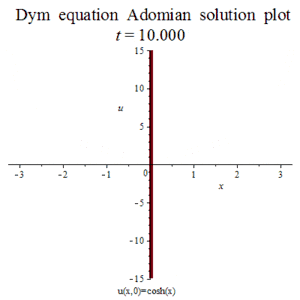
迪姆方程：

u_{t}=u^{3}u_{xxx}.\,

u[0]=cosh(x)

u[1]=-cosh(x)*sinh(x)*t

u[5]=-t^{5}*cosh(x)*sinh(x)^{5}-(20/3)*t^{5}*cosh(x)^{3}*sinh(x)^{3}-(47/15)*t^{5}*cosh(x)^{5}*sinh(x)

ADM近似：

u（x,t)~pa := (-.5382*sinh(10.*x)-.7224*sinh(8.*x)-.2441*sinh(6.*x)-0.5787e-4*sinh(2.*x)-0.1693e-1*sinh(4.*x))*t^9+(.4634*cosh(9.*x)+0.5933e-2*cosh(3.*x)+.5585*cosh(7.*x)+.1514*cosh(5.*x)+0.1356e-5*cosh(x))*t^8+(-.4063*sinh(8.*x)-0.8889e-1*sinh(4.*x)-.4339*sinh(6.*x)-0.1389e-2*sinh(2.*x))*t^7+(0.1085e-3*cosh(x)+0.4746e-1*cosh(3.*x)+.3647*cosh(7.*x)+.3391*cosh(5.*x))*t^6+(-0.2083e-1*sinh(2.*x)-.2667*sinh(4.*x)-.3375*sinh(6.*x))*t^5+(.3255*cosh(5.*x)+0.5208e-2*cosh(x)+.2109*cosh(3.*x))*t^4+(-.3333*sinh(4.*x)-.1667*sinh(2.*x))*t^3+(.3750*cosh(3.*x)+.1250*cosh(x))*t^2-.5000*t*sinh(2.*x)+cosh(x)

参考文献

George Adomian, Nonlinear Stochastic Systems and Application to Physics,Kluwer Academic Publisher
George Adomian,Solving Frontier Problems of Physics,The Decomposition Method,Boston, Kluwer Academic Publisher 1994

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] George Adomian, Nonlinear Stochastic Systems and Application to Physics,Kluwer Academic Publisher

[2] George Adomian,Solving Frontier Problems of Physics,The Decomposition Method,Boston, Kluwer Academic Publisher 1994