雅可比橢圓函數
介紹

雅可比矩形
雅可比橢圓函數有十二種,各對映到某個矩形的頂點連線。此諸頂點記作 。
視此矩形為複數平面的一部分, 是原點, 是實軸上的一點 是 , 是 。 與 稱作四分之一週期。
十二個橢圓函數分別記為 。為方便起見,取變數 意指矩形上的任一對頂點,則函數 是唯一滿足以下性質的週期亞純函數
- 是單零點, 是單極點。
- 在 方向的週期等於 距離的兩倍。對另兩個從 出發的方向,亦滿足同樣性質。
- 在頂點 的展式首項係數均為一。
表列如次:
| 函數 | 週期 | 零點 | 極點 | 留數 |
|---|---|---|---|---|
| 與 是整數 | ||||
一般而言,須以平行四邊形代替上述矩形,以考慮更一般的週期。
表為橢圓積分之逆
以上定義略顯抽象,更具體的定義是將之表為某類橢圓積分(第一類不完全橢圓積分)之逆。設
橢圓正弦函數 sn u 定義為
而橢圓余弦函數 cn u 定義為
同理,椭圆德尔塔函数有
這裡的 是自由變元,通常取 。
剩下的九種橢圓函數能由這三種構造。
反函數
雅可比椭圆函数的反函数可以像三角函数与反三角函数那样被定义。因为椭圆函数往往是椭圆积分之逆,这些反函数也都可以用勒让德椭圆积分来描述。如同反三角函数一样,雅可比椭圆函数的反函数也是多值的,因此需要支割线。以下是部分反函数的积分表达:
函数的平方之间的关系
图像
 |
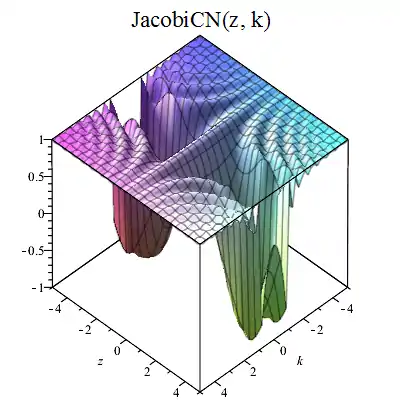 |
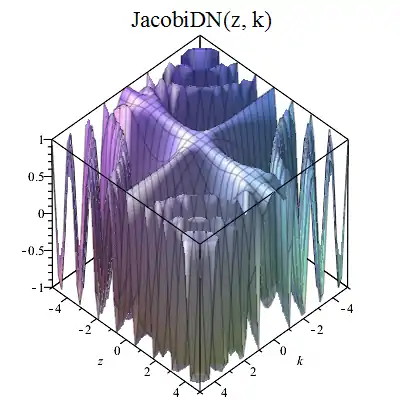 |
文獻
- Abramowitz, Milton; Stegun, Irene A. eds. . New York: Dover. 1972. ISBN 0-486-61272-4. 見 第16章 (页面存档备份,存于)
- Naum Illyich Akhiezer, Elements of the Theory of Elliptic Functions, (1970) Moscow, translated into English as AMS Translations of Mathematical Monographs Volume 79 (1990) AMS, Rhode Island ISBN 0-8218-4532-2
- E. T. Whittaker and G. N. Watson A Course of Modern Analysis, (1940, 1996) Cambridge University Press. ISBN 0-521-58807-3
- Alfred George Greenhill, The applications of elliptic functions (London, New York, Macmillan, 1892)
- H. Hancock Lectures on the theory of elliptic functions (New York, J. Wiley & sons, 1910)
- A. C. Dixon The elementary properties of the elliptic functions, with examples (Macmillan, 1894)
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.