雙曲函數恆等式
在数学中,雙曲函數恆等式是对出现的变量的所有值都为實的涉及到雙曲函數的等式。这些恒等式在表达式中有些雙曲函數需要简化的时候是很有用的。雙曲函數的恆等式有的與三角恆等式類似。就如同三角函數,他有一个重要应用是非雙曲函數的积分:一个常用技巧是首先使用换元积分法,規則與使用三角函数的代换规则類似,则通过雙曲函數恆等式可简化结果的积分。
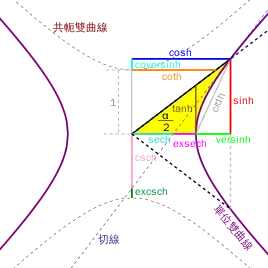
雙曲扇形a的很多雙曲函数可以在几何上依据以O为中心的雙曲線来构造。
符号
| 函数 | 倒數函数 | |||
|---|---|---|---|---|
| 全寫 | 簡寫 | 全寫 | 簡寫 | |
| 函数 | hyperbolic sine | sinh | hyperbolic cosecant | csch |
| 反函数 | inverse hyperbolic sine | arcsinh | inverse hyperbolic cosecant | arccsch |
| 函数 | hyperbolic cosine | cosh | hyperbolic secant | sech |
| 反函数 | inverse hyperbolic cosine | arccosh | inverse hyperbolic secant | arcsech |
| 函数 | hyperbolic tangent | tanh | hyperbolic cotangent | coth |
| 反函数 | inverse hyperbolic tangent | arctanh | inverse hyperbolic cotangent | arccoth |
基本關係

sinh, cosh 和 tanh
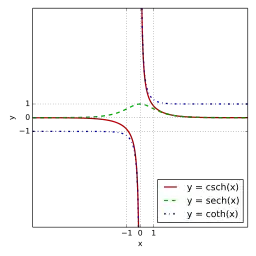
csch, sech 和 coth
雙曲函數基本恒等式如下:
就如同三角函數,由上面的平方關係加上雙曲函數的基本定義,可以導出下面的表格,即每個雙曲函數都可以用其他五個表達。(严谨地说,所有根号前都应根据实际情况添加正负号)
| 函數 | sinh | cosh | tanh | coth | sech | csch |
|---|---|---|---|---|---|---|
和角公式
和差化積公式
積化和差公式
倍角公式
- 二倍角公式:
- 三倍角公式:
半形公式
幂简约公式
雙曲正切半形公式
參考文獻
- 數學基本公式手冊 九章出版社 ISBN 957-603-010-2
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.