雪崩效应

在密码学中，雪崩效应（avalanche effect）指加密算法（尤其是块密码和加密散列函数）的一种理想属性。雪崩效应是指当输入发生最微小的改变（例如，反转一个二进制位）时，也会导致输出的不可区分性改变（输出中每个二进制位有50%的概率发生反转）。合格块密码中，无论密钥或明文的任何细微变化都必须引起密文的不可区分性改变。该术语最早由Horst Feistel使用，[1]尽管其概念最早可以追溯到克劳德·香农提出的扩散（diffusion）。

SHA-1散列函数展示了良好的雪崩效应。当一个二进制位发生变化时，散列校验和将随之而截然不同。

  此條目介紹的是密碼學中的雪崩效應。关于半導體的雪崩效應，请见「突崩潰」。

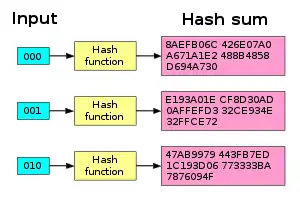
若某种块密码或加密散列函数没有显示出一定程度的雪崩特性，那么它被认为具有较差的随机化特性，从而密码分析者得以仅仅从输出推测输入。这可能导致该算法部分乃至全部被破解。因此，从加密算法或加密设备的设计者角度来说，满足雪崩效应乃是必不可缺的圭臬。

构造一个具备良好雪崩效应的密码或散列是至关重要的设计目标之一。这正是绝大多数块密码采用了乘积密码的原因，也是大多数散列函数使用大数据块的原因。这些特性均使得微小的变化得以通过算法的迭代迅速增殖，造成输出的每一个二进制位在算法终止前均受到输入的每一个二进制位的影响。