静力学

靜力學是经典力学的分支，专门解析物体在靜力平衡狀态下的负载（力量，力矩）。在这狀态下，或许有外力作用于此物体；但是，各個分系統的相对位置、成分、结构仍旧保持不变。当呈靜力平衡狀态时，系統或者是静止的，或者其質心维持常速运动，处于力学平衡状态。

處於靜力平衡狀态的横梁，其净力与净力矩皆为零。

在静力学上，靜力解析的焦点是放在比较靜力學，就是比较各种不同的靜力平衡狀态。它除了稍微提到外生变数造成的变动外，并不注重狀态间的過程。

设 ${\textbf {F}}$ 为施于系统上的合力， $m$ 为系统总质量， ${\textbf {a}}$ 为系统加速度，则依照牛顿运动第二定律有 ${\textbf {F}}=m{\textbf {a}}\,$ （粗体表示向量，即有方向的量）。

将加速度为零的假设应用于外力力矩求和，可得 ${\textbf {M}}=I\alpha =0$ ，其中 ${\textbf {M}}$ 是外力力矩之和， $I$ 是质量惯性矩， $\alpha$ 是系统的角加速度。对于 $\alpha =0$ 的系统，也有 ${\textbf {M}}=0.$

外净力 ${\textbf {F}}=m{\textbf {a}}=0$ 又称为靜力平衡第一条件，外净力矩 ${\textbf {M}}=I\alpha =0$ 又称为靜力平衡第二条件，可以用来求解作用于系统的未知量。

历史

阿基米德（c. 287–c. 212 BC）在静力学领域做了先驱工作。[1][2]萨比特的著作中有一些后来的工作。[3]

背景

力

力是物体对另一个物体的作用，可以是推力，也可以是拉力，趋向于使物体沿其作用方向移动。力的作用由其大小、作用方向和作用点决定。因此，力是一个矢量，因为其效果既取决于作用方向，也取决于作用大小。[4]

力分为接触力和体积力。接触力由直接物理接触产生，例如支撑表面对人体施加的力；体积力由体在力场（如引力场、电场或磁场）中的位置产生，与任何其他接触无关。地球引力场中的物体重量是体积力的一个例子。[5]

力矩

除了使物体沿作用方向移动的趋势外，力还能使物体绕轴旋转，轴线和力的方向之间是任意的。这种旋转趋势称作力矩（M），也称为扭矩。

关于点的力矩

力F的力臂示意图。

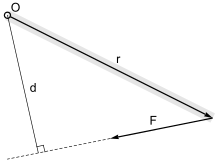
力在O点的力矩大小等于O到F作用线的距离乘以力的大小：M = F · d，其中

F = 施加的力

d = 从轴线到力的作用线的距离，称作力臂。

力矩的方向由右手定则给出，逆时针代表指出纸面，顺时针表示进入纸面。力矩方向可用符号约定表示，例如逆时针用正号（+）表示，顺时针用负号（−）表示，反之亦然。力矩可以矢量形式相加。

用向量形式来写，力矩可以定义为径向量r与力向量F的叉乘：[6]

{\textbf {M}}_{O}={\textbf {r}}\times {\textbf {F}}

r=\left({\begin{array}{cc}x_{00}&...&x_{0j}\\x_{01}&...&x_{1j}\\...&...&...\\x_{i0}&...&x_{ij}\\\end{array}}\right)

F=\left({\begin{array}{cc}f_{00}&...&f_{0j}\\f_{01}&...&f_{1j}\\...&...&...\\f_{i0}&...&f_{ij}\\\end{array}}\right)

伐里农定理

伐里农定理指出，力对任意点的力矩等于力对同一点各分力的力矩之和。

平衡方程

质点的静力平衡是静力学中的重要概念。只有当质点受外力为零时，质点才处于平衡状态。在矩形坐标系中，平衡方程可用3个标量方程表示，3个方向的合力都等于零。这概念在工程上的应用是确定3根缆绳在负载下的张力，例如提升物体的升降机或将热气球固定在地面上的缆绳上施加的力。[7]

转动惯量

经典力学中，转动惯量（SI单位kg·m²），是物体对其旋转变化的阻力的量度，是旋转体相对于其旋转的惯性。转动惯量在旋转动力学中的作用与质量在线性动力学中的作用大致相同，描述了角动量与角速度、转矩与角加速度以及其他几个量之间的关系。I 和 J 通常指惯性矩或极惯性矩。

虽然转动惯量的简单标量处理在许多情况下已经足够，但更高级的张量处理可以分析陀螺运动等复杂系统。

这一概念由莱昂哈德·欧拉在《天体运动论》（1765）一书中提出；他讨论了转动惯量和许多相关概念，如惯性主轴。

应用

固体

靜力學在分析结构上是很重要的。举例而言，在建筑学与结构工程学里，材料的强度常需应用到靜力平衡。一个关键概念是质心，即物体所有质量所在的假想点。质心所在的地基位置决定了物体在外力作用下的稳定性。若质心在地基之外，物体就不稳，因为有扭矩起作用：任何微扰都会使物体下坠或倾覆。若质心在地基内，则物体稳定，因为没有净扭矩作用在物体上。若质心与地基重合，则称系统处于准稳态。

流体

流体静力学研究静止狀态下的液體。静态液體的特性是内部每个分子所受的力在任何方向都是同值的。否则，液體会往净力向量的方向流去。这概念是由法国数学家布莱兹·帕斯卡在1647年提出的，后来又称为帕斯卡定律。它在水力学中有许多重要应用。阿基米德、比鲁尼、Al-Khazini[8]和伽利略·伽利莱在靜力學上也有很大的贡献。

参阅

注释

Lindberg, David C. . Chicago: The University of Chicago Press. 1992: 108-110. ISBN 9780226482316.
Grant, Edward. . New York: Cambridge University Press. 2007: 309-10.
Holme, Audun. 2nd. Heidelberg: Springer. 2010: 188. ISBN 978-3-642-14440-0.
Meriam, James L., and L. Glenn Kraige. Engineering Mechanics (6th ed.) Hoboken, N.J.: John Wiley & Sons, 2007; p. 23.
Engineering Mechanics, p. 24
Hibbeler, R. C. . New Jersey: Pearson Prentice Hall. 2010. ISBN 978-0-13-607790-9.
Beer, Ferdinand. . McGraw Hill. 2004. ISBN 0-07-121830-0.
Mariam Rozhanskaya and I. S. Levinova (1996), "Statics", p. 642, in （Morelon & Rashed 1996，pp.614–642）:
“阿拉伯科学家利用一整套数学方法（不仅包括从古代比率论和小量技术中继承下来的方法，还包括当代代数方法和精细计算技术）将静力学提高到了更高水平。阿基米德重心理论的古典成果得到了推广，应用于三维物体，建立了可量杠杆理论，创立了‘重力科学’，后来在中世纪欧洲得到进一步发展。用动力学方法研究静力学现象的过程中，静力学和动力学这两种趋势逐渐形成了力学这门单一科学。动力学方法与阿基米德流体力学的结合产生了所谓‘中世纪流体力学’。[...]为称量特定的重量，人们发明了许多试验方法，尤以天平和称量理论为基础。al-Biruni和al-Khazini的经典著作可被视为实验方法在中世纪科学中应用的开端。”

参考文献

Beer, F.P. & Johnston Jr, E.R. . McGraw-Hill, Inc. 1992.
Beer, F.P.; Johnston Jr, E.R.; Eisenberg. . McGraw Hill. 2009. ISBN 978-0-07-352923-3.
Morelon, Régis; Rashed, Roshdi (编), 3, Routledge, 1996, ISBN 978-0415124102

外部链接

教育部进修网站，静力学

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Lindberg, David C. . Chicago: The University of Chicago Press. 1992: 108-110. ISBN 9780226482316.

[2] Grant, Edward. . New York: Cambridge University Press. 2007: 309-10.

[holme-3] Holme, Audun. 2nd. Heidelberg: Springer. 2010: 188. ISBN 978-3-642-14440-0.

[4] Meriam, James L., and L. Glenn Kraige. Engineering Mechanics (6th ed.) Hoboken, N.J.: John Wiley & Sons, 2007; p. 23.

[5] Engineering Mechanics, p. 24

[6] Hibbeler, R. C. . New Jersey: Pearson Prentice Hall. 2010. ISBN 978-0-13-607790-9.

[7] Beer, Ferdinand. . McGraw Hill. 2004. ISBN 0-07-121830-0.

[Rozhanskaya-642-8] Mariam Rozhanskaya and I. S. Levinova (1996), "Statics", p. 642, in （Morelon & Rashed 1996，pp.614–642）:
“阿拉伯科学家利用一整套数学方法（不仅包括从古代比率论和小量技术中继承下来的方法，还包括当代代数方法和精细计算技术）将静力学提高到了更高水平。阿基米德重心理论的古典成果得到了推广，应用于三维物体，建立了可量杠杆理论，创立了‘重力科学’，后来在中世纪欧洲得到进一步发展。用动力学方法研究静力学现象的过程中，静力学和动力学这两种趋势逐渐形成了力学这门单一科学。动力学方法与阿基米德流体力学的结合产生了所谓‘中世纪流体力学’。[...]为称量特定的重量，人们发明了许多试验方法，尤以天平和称量理论为基础。al-Biruni和al-Khazini的经典著作可被视为实验方法在中世纪科学中应用的开端。”