韦伯分布

**韦伯分布**
	密度函數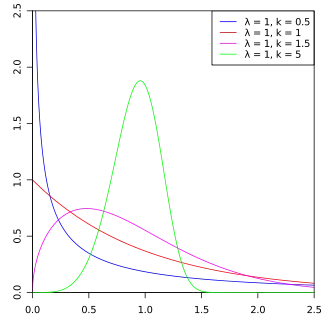
	累積分布函數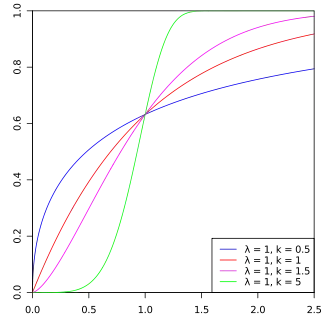
	尺度参数（实数）; 形状参数（实数）
值域
累積分布函數
期望值
中位數
眾數	if
偏度
峰度	见内文
熵
特徵函数

韦伯分布（Weibull distribution）是可靠性分析和寿命检验的理论基础。

例如，可以使用此分布回答以下问题：

预计将在老化期间失效的项目所占的百分比是多少？例如，预计将在 8 小时老化期间失效的保险丝占多大百分比？

预计在有效寿命阶段有多少次保修索赔？例如，在该轮胎的 50,000 英里有效寿命期间预计有多少次保修索赔？

预计何时会出现快速磨损？例如，应将维护定期安排在何时以防止发动机进入磨损阶段？

历史

1927年，莫里斯·弗雷歇首先给出这一分布的定义。

1933年，Rosin, P.和Rammler, E.在研究碎末的分布时，第一次应用了韦伯分布。

1951年，瑞典工程师、数学家瓦洛迪·韦伯详细解释了这一分布，于是，该分布便以他的名字命名为韦伯分布。

定义

从概率论和统计学角度看，韦伯分布是连续性的概率分布，其概率密度为：

f(x;\lambda ,k)={\begin{cases}{\frac {k}{\lambda }}\left({\frac {x}{\lambda }}\right)^{k-1}e^{-({\frac {x}{\lambda }})^{k}}&x\geq 0\\0&x<0\end{cases}}

其中， $x$ 是随机变量， $\lambda >0$ 是比例参数（scale parameter）， $k>0$ 是形状参数（shape parameter）。显然，它的累积分布函数是扩展的指数分布函数，而且韦伯分布与很多分布都有关系。如，当 $k=1$ ，它是指数分布； $k=2$ 时，是Rayleigh distribution（瑞利分布）。

性质

均值

$E=\lambda \Gamma \left(1+{\frac {1}{k}}\right)\,$ 其中， $\Gamma$ 是伽马（gamma）函数。

方差

$Var=\lambda ^{2}\left[\Gamma \left(1+{\frac {2}{k}}\right)-\Gamma \left(1+{\frac {1}{k}}\right)^{2}\right],$

偏度

$skewness={\frac {2\Gamma \left(1+{\frac {1}{k}}\right)^{3}-3\Gamma \left(1+{\frac {2}{k}}\right)\Gamma \left(1+{\frac {1}{k}}\right)+\Gamma \left(1+{\frac {3}{k}}\right)}{\left[\Gamma \left(1+{\frac {2}{k}}\right)-\Gamma \left(1+{\frac {1}{k}}\right)^{2}\right]^{\frac {3}{2}}}}$

峰度

$kurtosis={\frac {-3\Gamma \left(1+{\frac {1}{k}}\right)^{4}+6\Gamma \left(1+{\frac {2}{k}}\right)\Gamma \left(1+{\frac {1}{k}}\right)^{2}-4\Gamma \left(1+{\frac {3}{k}}\right)\Gamma \left(1+{\frac {1}{k}}\right)+\Gamma \left(1+{\frac {4}{k}}\right)}{\left[\Gamma \left(1+{\frac {2}{k}}\right)-\Gamma \left(1+{\frac {1}{k}}\right)^{2}\right]^{2}}}$

应用

工业制造

研究生产过程和运输时间关系

雷达系统

对接受到的杂波信号的依分布建模

拟合度

无线通信技术中，相对指数衰减频道模型，Weibull衰减模型对衰减频道建模有较好的拟合度

风速

由于曲线形状与现实状况很匹配，被用来描述风速的分布

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

**韦伯分布**
密度函數
累積分布函數
	$\lambda >0\,$ 尺度参数（实数） $k>0\,$ 形状参数（实数）
值域	$x\in [0;+\infty )\,$
	$f(x)={\begin{cases}{\frac {k}{\lambda }}\left({\frac {x}{\lambda }}\right)^{k-1}e^{-(x/\lambda )^{k}}&x\geq 0\\0&x<0\end{cases}}$
累積分布函數	$1-e^{-(x/\lambda )^{k}}$
期望值	$\lambda \Gamma \left(1+{\frac {1}{k}}\right)\,$
中位數	$\lambda (\ln(2))^{1/k}\,$
眾數	$\lambda \left({\frac {k-1}{k}}\right)^{\frac {1}{k}}\,$ if $k>1$
	$\lambda ^{2}\Gamma \left(1+{\frac {2}{k}}\right)-\mu ^{2}\,$
偏度	${\frac {\Gamma (1+{\frac {3}{k}})\lambda ^{3}-3\mu \sigma ^{2}-\mu ^{3}}{\sigma ^{3}}}$
峰度	见内文
熵	$\gamma \left(1\!-\!{\frac {1}{k}}\right)+\ln \left({\frac {\lambda }{k}}\right)+1$
	$\sum _{n=0}^{\infty }{\frac {t^{n}\lambda ^{n}}{n!}}\Gamma \left(1+{\frac {n}{k}}\right),\ k\geq 1$
特徵函数	$\sum _{n=0}^{\infty }{\frac {(it)^{n}\lambda ^{n}}{n!}}\Gamma \left(1+{\frac {n}{k}}\right)$