頂點 (幾何)
在幾何學中,頂點是2條或以上的邊、超邊、線、線段或曲線等數學物件的交會點。在這個定義之下,多面體或多邊形中由2條邊或稜所交出的角或頂角其端點稱為一個頂點[1]。在抽象幾何學中,頂點是抽象多胞形中的0維元素。[2]
定義
角的頂點
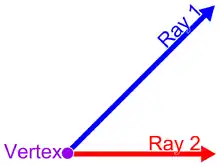
角是由兩條有公共端點的射线組成的幾何物件。這兩條射線叫做角的邊,它們的公共端點叫做角的頂點[3]。角的頂點也可以是下列定義的其中之一:
- 2條射線的起始點或交點
- 2條線段的連接或交點
- 2條直線的交點
多胞形的頂點
頂點是多邊形、多面體或其他高維多胞體的角之端點。為幾何結構的邊、面或維面相交形成的交點。[4]而包含該頂點的組成之數學物件整體稱為一個頂角,其在英語中皆稱為Vertex,而頂點圖(Vertex figure)探討的則為頂角的特性,而非只探討頂點本身。[5]
在多邊形中,若一個頂點對應到的頂角,其內角小於180度則稱該頂點為凸頂點,否則為凹頂點。[6]更一般地,如果一個n維幾何體的其中一個頂點可以使這個幾何體與位於這個頂點上之充分地小的n維球體相交的話,則這個頂點為凸頂點[7]。
多胞形的頂點可以對應到圖論中的頂點,因為任何多胞形皆可以找到一個對應的邊與頂點的圖[8],而這個幾何物件正是圖論中的一種數學物件,其頂點可以對應於原始多胞形中的頂點[9],而這個圖可以被視為一維单纯复形,其頂點正是一個圖頂點。然而,在圖論中,頂點有可能少於兩條邊(如自環),而在幾何中無法存在這種頂角。幾何頂點和曲線的頂點之間也有關聯。曲線的頂點通常代表曲線的局部極值[10],在某種意義上,多邊形的頂點是無限曲率的點,並且若用平滑曲線來近似一個多邊形,則在多邊形的每個頂點附近將存在極端曲率的點。[11]
多面體的頂點
在多面體中,頂點是多面體中3個或以上的面的交會點。一般情況下,多面體頂點的數量可透過歐拉特徵數計算得出。任何凸多面體表面的歐拉特徵皆符合下列等式:
其中V是頂點數、E是邊數、F是面數。這個等式稱為歐拉恆等式[12],由此可知,邊的數量恆比頂點和面的數量的總和小2。例如,立方體有12條邊和6個面,因此根據歐拉恆等式可以得到有立方體有8個頂點。
平面鑲嵌的頂點
平面鑲嵌的頂點是三個過更多個鑲嵌元素(即拼出平面鑲嵌的單個幾何圖形)的交會點[13]。平面鑲嵌通常由多邊形組成,且平面鑲嵌的頂點同時也是多邊形的頂點,然而有例外存在。
 多邊形的頂點同時也是平面 鑲嵌的頂點之例子 |
 其中一個反例 |
主頂點
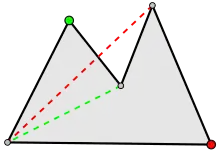
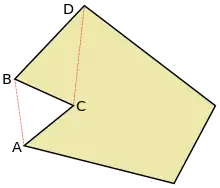
在多邊形中,主頂點(Principal Vertex)是指多邊形中的一個頂點,該頂點相鄰兩頂點的對角線不與多邊形邊界相交。更正式的定義如下:有一個簡單多邊形P,其有頂點 {x1, x2, ..., xp-1, xp} ,其中xp+1=x1使多邊形P為封閉結構。在多邊形P中,若存在一個頂點xi使得多邊形P的對角線 [x(i − 1), x(i + 1)] 僅在x(i − 1)點與x(i + 1)點上與P的邊界相交,則稱頂點xi為該多邊形的主頂點。 主頂點可以分成兩種類型:耳頂點和嘴頂點。[14]
耳頂點
若一主頂點對應的對角線位於多邊形內部,則這個頂點稱為耳頂點。根據雙耳定理,任何簡單多邊形都至少會有2個耳頂點。[15]
嘴頂點
若一主頂點對應的對角線位於多邊形外部,則這個頂點稱為嘴頂點。[16]

在中,三維幾何結構(在一般稱為模型)通常會表示為以三角形構成的多面體,其中,頂點所包含的資訊不像幾何學中只含有座標資訊,而會額外地包含其渲染所需的資訊,如顏色、反射特性、紋理和表面法線等[17]。這些頂點的屬性會輸入到頂點著色器,進而開始的渲染流程。
參見
參考文獻
- Weisstein, Eric W. (编). . at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- McMullen, Peter; Schulte, Egon, 1st, Cambridge University Press, December 2002, ISBN 0-521-81496-0
- Sidorov, L. A., , Hazewinkel, Michiel (编), , Springer, 2001, ISBN 978-1-55608-010-4
- Heath, Thomas L. 2nd ed. [Facsimile. Original publication: Cambridge University Press, 1925]. New York: Dover Publications. 1956.
- Olshevsky, George, Vertex figure at Glossary for Hyperspace.
- Jing, Lanru; Stephansson, Ove. . Elsevier Science. 2007.
- Gruber, P.M. . Grundlehren der mathematischen Wissenschaften. Springer Berlin Heidelberg. 2007. ISBN 9783540711339. LCCN 2007922936.
- Senechal, Marjorie, , Springer: 81, 2013 [2019-09-15], ISBN 9780387927145, (原始内容存档于2014-01-07).
- Peter McMullen, Egon Schulte, Abstract Regular Polytopes, Cambridge University Press, 2002. ISBN 0-521-81496-0 (Page 29)
- Gibson, C. G., , Cambridge University Press: p. 127, 2001, ISBN 9780521011075
- Bobenko, Alexander I.; Schröder, Peter; Sullivan, John M.; Ziegler, Günter M. . Birkhäuser Verlag AG. 2008. ISBN 978-3-7643-8620-7.
- Richeson, David S.; Euler's Gem: The Polyhedron Formula and the Birth of Topology. Princeton University Press 2008.
- M.V. Jaric, ed, Introduction to the Mathematics of Quasicrystals (Aperiodicity and Order, Vol 2) ISBN 0-12-040602-0, Academic Press, 1989
- . McGill School Of Computer Science, McGill University. [2019-09-15]. (原始内容存档于2021-02-07).
- Meisters, G. H., , The American Mathematical Monthly, 1975, 82: 648–651, MR 0367792, doi:10.2307/2319703.
- Toussaint, Godfried, , American Mathematical Monthly, 1991, 98 (1): 31–35, MR 1083611, doi:10.2307/2324033.
- Christen, Martin. . Khronos Group. [26 January 2009]. (原始内容存档于2019-04-12).
- Von Zelewsky, A. . Chichester: John Wiley. 1995. ISBN 0-471-95599-X.
- D. L. Kepert. . Progress in Inorganic Chemistry. 1978, 24: 179–249. doi:10.1002/9780470166253.ch4.