黄金分割法
0.618法,又叫黄金分割法,是优选法的一种。它在试验时,把试点安排在黄金分割点上来寻找最佳点。而生产生活中,我们常常取其近似值0.618,因此得名。0.618法是最常用的单因素单峰目标函数优选法之一。 [1] [2]
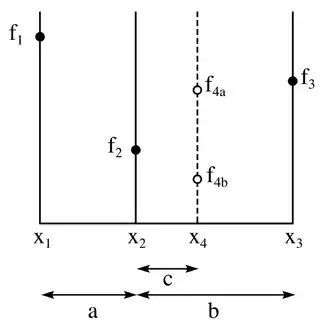
黄金分割法示意图
精度
用0.618法寻找最佳点时,虽然不能保证在有限次内准确找出最佳点,但随着试验次数的增加,最佳点被限定在越来越小的范围内,即存优范围会越来越小。用存优范围与原始范围的比值来衡量一种试验方法的效率,这个比值叫精度。用0.618法确定试点时,每一次实验都把存优范围缩小为原来的0.618.因此,n次试验后的精度为:
一般地,如果给定一个精度,用0.618法进行的试验次数是:
取整数。[5]
参考资料
- Kiefer, J., , Proceedings of the American Mathematical Society, 1953, 4 (3): 502–506, JSTOR 2032161, MR 0055639, doi:10.2307/2032161
- Avriel, Mordecai; Wilde, Douglass J., , Fibonacci Quarterly, 1966, 4: 265–269, MR 0208812
- 白寿彝. . . 上海人民出版社. ISBN 7208049971.
- 课程教材研究所 中学数学课程教材研究开发中心. . 人民教育出版社. 2009年3月: 44. ISBN 978-7-107-19170-1.
著名数学家华罗庚曾为普及它作出重要贡献.
- 刘少学. . 人民教育出版社. 2007年1月: 9. ISBN 978-7-107-18682-0.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.