AC自动机算法
在计算机科学中,艾侯-科拉希克算法(英語:)是由阿尔佛雷德·艾侯和玛格丽特·J·科拉希克(Margaret J. Corasick)发明的字符串搜索算法,[1]用于在输入的一串字符串中匹配有限组“字典”中的子串。它与普通字符串匹配的不同点在于同时与所有字典串进行匹配。算法均摊情况下具有近似于线性的时间复杂度,约为字符串的长度加所有匹配的数量。然而由于需要找到所有匹配数,如果每个子串互相匹配(如字典为a,aa,aaa,aaaa,输入的字符串为aaaa),算法的时间复杂度会近似于匹配的二次函数。
| AC自动机算法 | |
|---|---|
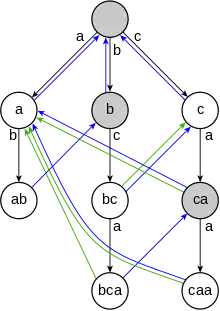 艾侯-科拉希克自动机示意图 | |
| 概况 | |
| 類別 | 字符串搜索、字符串匹配 |
| 資料結構 | 字符串有限状态机 |
| 复杂度 | |
| 相关变量的定义 | |
该算法主要依靠构造一个有限状态机(类似于在一个trie树中添加失配指针)来实现。这些额外的失配指针允许在查找字符串失败时进行回退(例如设Trie树的单词cat匹配失败,但是在Trie树中存在另一个单词cart,失配指针就会指向前缀ca),转向某前缀的其他分支,免于重复匹配前缀,提高算法效率。
当一个字典串集合是已知的(例如一个计算机病毒库), 就可以以离线方式先将自动机求出并储存以供日后使用,在这种情况下,算法的时间复杂度为输入字符串长度和匹配数量之和。
样例
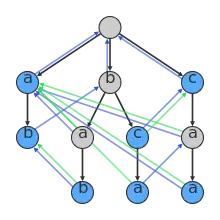
设一个字典中有如下单词:{a,ab,bab,bc,bca,c,caa}.
下方的图是用AC自动机算法由该词典构造而成的一棵Trie树,其中每个节点都有一条从根节点到它的唯一路径,代表一个单词。
在这种数据结构中,字符串的每一个前缀都有一个节点来表示(详见Trie)。所以如果(bca)在字典中,则会存在(bca),(bc),(b)和()对应的节点。如果该节点表示的字符串在字典中存在,则该节点为一个蓝色节点,否则为一个灰色节点。
树中的黑色有向边代表起点是终点的“父亲”(即起点对应字符串增加一个字符可得终点对应字符串),例如从(bc)有一条指向(bca)的黑色有向边。
树中的蓝色有向边(后缀节点)代表终点对应字符串是起点对应字符串的最大严格后缀。例如对于一个节点(caa),它的严格后缀为(aa),(a)和(),其中在图中且最长的为(a),所以(caa)有一条指向(a)的蓝色有向边。一个节点的蓝色有向边可以在线性时间内通过重复遍历节点父亲节点的蓝色有向边直到横移节点(the traversing node)有一个属于目标节点前缀的孩子。
树中的绿色有向边(字典后缀节点)代表终点是起点经过蓝色有向边到达的第一个蓝色节点(即字典中存在终点对应字符串)。例如(bca)有一条绿色边连向(a),因为(a)是(bca)通过蓝色有向边到达的第一个蓝色节点,路径为(bca)→(ca)→(a)。绿色有向边也可以在线性时间内通过遍历蓝色有向边直到找到一个蓝色节点,并用记忆化的方法计算。
| 节点 | 是否在字典中 | 后缀节点(蓝色有向边) | 字典后缀节点(绿色有向边) |
|---|---|---|---|
| () | – | ||
| (a) | + | () | |
| (ab) | + | (b) | |
| (b) | – | () | |
| (ba) | – | (a) | (a) |
| (bab) | + | (ab) | (ab) |
| (bc) | + | (c) | (c) |
| (bca) | + | (ca) | (a) |
| (c) | + | () | |
| (ca) | – | (a) | (a) |
| (caa) | + | (a) | (a) |
在每一步中,算法先查找当前节点的“孩子节点”,如果没有找到匹配,查找它的後缀(suffix)节点的孩子,如果仍然没有,接着查找後缀节点的後缀节点的孩子,如此循環,直到根結點,如果到达根节点仍没有找到匹配则结束。
当算法查找到一个节点,则输出所有结束在当前位置的字典项。输出步骤为首先找到该节点的字典后缀,然后用递归的方式一直执行到节点没有字典前缀为止。同时,如果该节点为一个字典节点,则输出该节点本身。
输入abccab后算法的执行步骤如下:
| 节点 | 剩余字符串 | 输出:结束位置 | 过渡 | 输出 |
|---|---|---|---|---|
| () | abccab | 从根开始 | ||
| (a) | bccab | a:1 | ()→子节点(a) | 当前节点 |
| (ab) | ccab | ab:2 | (a)→子节点(ab) | 当前节点 |
| (bc) | cab | bc:3, c:3 | (ab)→后缀节点(b)→子节点(bc) | 当前节点,字典后缀 |
| (c) | ab | c:4 | (bc)→后缀节点(c)→后缀节点()→子节点(c) | 当前节点 |
| (ca) | b | a:5 | (c)→(ca) | 字典后缀 |
| (ab) | ab:6 | (ca)→后缀节点(a)→子节点(ab) | 当前节点 |
参考来源
- Aho, Alfred V.; Corasick, Margaret J. . Communications of the ACM. June 1975, 18 (6): 333–340. MR 0371172. doi:10.1145/360825.360855.
外部链接
- Set Matching and Aho–Corasick Algorithm, lecture slides by Pekka Kilpeläinen
- Aho–Corasick entry(页面存档备份,存于) in NIST's Dictionary of Algorithms and Data Structures
- Aho-Corasick implementation in C++(页面存档备份,存于)
- Aho-Corasick implementation in Go(页面存档备份,存于)