升壓變換器
升壓變換器也稱為boost變換器或升壓斬波器,是可以提昇電壓的DC-DC轉換器,其輸出(負載)電壓會比輸入(電源)電壓要高。升壓變換器是屬於至少有二個半導體元件(一個二極體及一個電晶體)及至少一個儲能元件(電感器)的開關電源。為了降低電壓漣波,會在輸入端及輸出端加裝用電容器製作(有時也會配合電感器)的濾波器。
簡介
升壓變換器的電源可以用任何適合的直流電源,例如電池、太陽能板、整流器或是直流發電機等。DC-DC轉換器可以將某個電壓的直流電轉換為不同電壓的直流電。升壓變換器是會提高電壓的DC-DC轉換器,其輸出電壓會較輸入電壓要高。不過因為功率()必須守恆,即使在假設效率為100%的條件下,其輸出電流都會小於輸入電流。
歷史
開關電源為了要有高效率,其開關需要快速的打開及關閉,而且損失要低。1950年代商用半導體開關的發明對開關電源非常重要,因此像升壓變換器之類的開關電源才得以進行。主要的DC-DC轉換器技術是在1960年代初期,可以購得半導體開關時發展的。航天產業需要體積小、輕量化而且高效率的電源轉換器,因此開關電源快速發展。
像開關電源之類的切換式系統在設計上是一大挑戰,因為其型態和開關何時導通、何時斷路有關。加利福尼亞理工學院的R. D. Middlebrook在1977年出版了現今使用的DC-DC轉換器模型。Middlebrook將每一個開關狀态下的電流組態用一種叫做狀態空間平均(state-space averaging)的方式加以平均。因此將二個(開關導通時、開關斷路時)不同的系統方程式變成一個。新的模型帶來有见地的设计方程,也帶動了開關電源的成長。
應用
電池供電的系統一般會將電池串聯來提較高的電壓,不過在許多高電壓的應用中,因為空間限制,無法用足夠多個的電池串聯到所需的電壓。升壓變換器可以提昇電壓,減少所需的電池數量。像電動車及照明系統就是利用電池再配合升壓變換器供電的系統。
NHW20的豐田普銳斯混合動力車使用500V的電動機,若沒有升壓變換器,需要使用將近417個電池來驅動電動機,不過豐田普銳斯只用了168個電池,再利用升壓變換器將電池總電壓從202 V提昇到500 V。升壓變換器也可以用來作一些較小型設備的供電,例如可攜式照明系統,像白光LED一般需要3.3V才能發光,配合升壓變換器可以用鹼式電池提供的1.5V電壓,升壓後再供電。
有一種稱為焦耳小偷的電路就是利用未穩壓的升壓變換器作為增壓的機制。此電路架構用在低電壓的電池應用中,目的在於利用升壓變換器來取得電池中殘餘的電力。當電池幾乎沒電時,因為電壓不夠,無法驅動一般負載,此時電池的殘餘電力就浪費了。
電路分析

升壓變換器的基本原理就是利用電抗器在電流變化時會產生或消除磁場,來抵抗電流的變化。 在升壓變換器中,輸出電壓恆大於輸入電壓,圖1為其線路圖。
(a)當開關導通時(S-ON),電流以順時針的方向經過電感器,電感器開始產生磁場來儲存能量,電感器的左側為正極。
(b)當開關開路時(S-OFF),因為其阻抗較大,電流會下降,之前產生的磁場會慢慢減少,設法提供負載的電流。電感器的極性會倒轉(左側變為為負極)。因此二個電壓源會疊加,經過二極體來為電容器充電。
若開關切換的夠快,電感器在二次的充電之間,不會完全放電到零電壓,若開關開路時(S-OFF),負載會持續接收到比輸入電壓要大的電壓。此時和負載並聯的電容器也同時充電,若開關導通時(S-ON),二極體逆向偏壓無法導通,此時就由電容器來提供負載電源。而且二極體也避免電容器透過導通的開關來放電。當然開關需要很快的再開路,以免電容器放電過多。
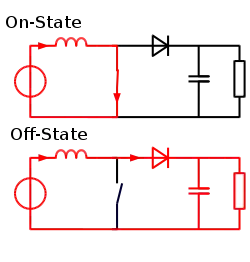
升壓變換器的基本原理包括二個不同的狀態(參考圖2):
- On狀態時,開關導通(S-ON)(參考圖2上半),因此電感器的電流增加。
- Off狀態時,開關開路(S-OFF)(參考圖2下半),電感器的電流只能經由飛輪二極體D、電容器C及負載這個路徑,此時電容器的能量會漸漸增加。
- 在圖2時輸入電流的大小和流經電感器的電流相同,輸入電流會變化,但不會像降壓變換器一様,有輸入電流不連續的問題,相較於降壓變換器,升壓變換器的輸入濾波器規格可以低一些。
連續模式

升壓變換器的連續模式是指在運作時電感器電流()不會降到零,圖3為此模式下的電壓及電流。 輸出電壓可以用以下方法計算,假設使用的是理想元件,在穩態下操作[1]:
在On狀態時,開關S導通,使電感器兩端的電壓即為輸入電壓,使電感器的電流()依下式變化:
在On狀態的最後,電流的總增加量為:
D為占空比,代表開關導通時間相對導通週期T的比例,因此D的範圍在0(S完全不導通)到1(S完全導通)之間。
在Off狀態時,開關S開路,電抗器的電流會流到負載端,若假設二極體的壓降為0,電容器的容值夠大,使輸出電壓可以維持定值,則IL的變化為:
因此在Off狀態電流的變化為:
因為假設升壓變換器是運作在穩態下,各元件儲能會在切換週期中變化,但在切換週期的開始及最後,各元件的儲能會相同,電感器的儲能為:
因此,電感器的電流在切換週期一開始及結束時需相等,因此總電流變化為零:
將及用輸入電壓及輸出電壓表示,可得:
可以寫成:
上式可以看出輸出電壓恆大於輸入電壓(因為占空比是在0到1之間),而且會隨D而增加,若D接近1時,轉換比例理論上會趨近無限大
改寫上述公式可得:
不連續模式
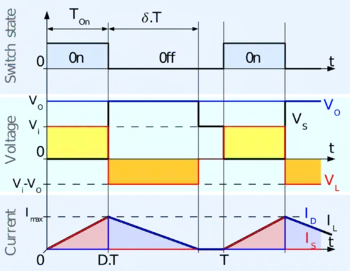
若電流漣波太大,電感器的電流可能在切換週期結束前就已降到零。這一般會出現在輕載的情形下,在圖4中,在切換週期最後會有一段時間的電感器電流為0。雖然看似輕微,不過這影響會對輸出電壓的方程有很大的影響。可以用以下方計算:
若在週期開始時,電感器電流為零,其最大值為(在時)為
在off期間,在時間後,IL會降到零:
利用上述二式可得:
負載電流Io等於平均二極體電流。如圖4所見,二極體電流等於在off期間的電感器電流,因此輸出電流如下:
將ILmax及δ改為其他算式,可得:
因此,輸出電壓增益為:
上式比連續模式下的輸出電壓要複雜多了,而且輸出電壓增益不止和占空比有關,也和電感器感值(L)、輸入電壓(Vi)、切換週期(T)及輸出電流(Io)。

