PBKDF2

PBKDF2 将伪随机函数（例如基于散列的消息身份验证码，HMAC）与盐值一起应用于输入密码或密码词组，并多次重复该过程以生成派生密钥，然后可以将其用作后续过程的加密密钥。增加的计算工作使密码破解变得更加困难，这被称为密钥延伸 。

在2000年编写的标准建议最小迭代次数为1,000次，但随CPU性能的提高，该参数会随着时间的推移而增加。2005年的Kerberos标准推荐4,096次迭代；[1]据报道，蘋果公司在iOS 3中使用了2,000次，在iOS 4中使用了10,000次；[4]而LastPass在2011年对JavaScript客户端使用了5,000次迭代，对服务器端哈希使用了100,000次迭代。[5] 2023 年，OWASP建议PBKDF2-HMAC-SHA256使用600,000次迭代，PBKDF2-HMAC-SHA512使用210,000 次迭代。[6]

PBKDF 2迭代过程的算法表示。

在密码中添加盐会降低使用预计算的哈希值（彩虹表）进行攻击的能力，并且意味着必须单独测试多个密码，而不是一次测试所有密码。该标准建议盐长度至少为64位。[7]美国国家标准与技术研究所推荐的长度为128位。 [8]

PBKDF2密钥推导函数有五个输入参数：[9]

DK = PBKDF2(PRF, Password, Salt, c, dkLen)

其中

• PRF 是一个有两个输入参数的伪随机函数（例如一个有密钥的HMAC），输出长度hLen
• Password 是主密码，推导密钥由它生成
• Salt 是一个比特序列，即盐
• c 是希望进行的迭代次数
• dkLen 是希望生成推导密钥的长度（位）
• DK 是生成的推导密钥

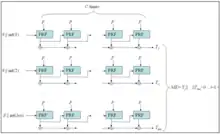
派生密钥DK的每个hLen位的块T_i计算如下（使用+表示字符串拼接）：

DK = T₁ + T₂ + ⋯ + T_dklen/hlen

T_i = F(Password, Salt, c, i)

函数F是链式PRF的c次迭代的异或( ^ )。PRF的第一次迭代使用Password作为PRF密钥，并将Salt与编码为大端序32位整数的i（索引i从1开始）拼接，作为输入。 PRF的后续迭代使用Password作为 PRF 密钥，并将先前PRF计算的输出作为输入：

F(Password, Salt, c, i) = U₁ ^ U₂ ^ ⋯ ^ U_c

其中

U₁ = PRF(Password, Salt + INT_32_BE(i))

U₂ = PRF(Password, U₁)

⋮

U_c = PRF(Password, U_c−1)

例如， WPA2使用：

DK = PBKDF2(HMAC−SHA1, passphrase, ssid, 4096, 256)

PBKDF1过程更简单：初始U （在这个版本中称为T ）由PRF(Password + Salt)创建，后面只是将上一轮的U作为下一轮PRF的输入，即PRF(U_previous) 。最后提取最终哈希的前dkLen位作为密钥。因此PBKDF1存在大小限制。[9]

当使用 HMAC 作为其伪随机函数时，PBKDF2 有一个有趣的特性。可以简单地构造任意数量的不同密码对，并且每对密码对都存在冲突。[10]如果提供的密码长于底层HMAC散列函数的块大小，则密码首先被预散列为摘要，然后该摘要用作密码。例如，以下密码太长：

• 密码： plnlrtfpijpuhqylxbgqiiyipieyxvfsavzgxbbcfusqkozwpngsyejqlmjsytrmd

因此，在使用 HMAC-SHA1 时，使用 SHA-1 将其预散列为：

• SHA1 （十六进制）： 65426b585154667542717027635463617226672a

可以用 ASCII 表示为：

• SHA1 （ASCII）： eBkXQTfuBqp'cTcar&g*

这意味着无论盐或迭代次数如何，PBKDF2-HMAC-SHA1 都会为下列密码生成相同的密钥字节：

• "plnlrtfpijpuhqylxbgqiiyipieyxvfsavzgxbbcfusqkozwpngsyejqlmjsytrmd"
• "eBkXQTfuBqp'cTcar&g*"

例如，使用：

• PRF : HMAC-SHA1
• 盐： A009C1A485912C6AE630D3E744240B04
• 迭代次数： 1,000
• 派生密钥长度： 16 字节

下面两个函数调用：

PBKDF2-HMAC-SHA1("plnlrtfpijpuhqylxbgqiiyipieyxvfsavzgxbbcfusqkozwpngsyejqlmjsytrmd", ...)
PBKDF2-HMAC-SHA1("eBkXQTfuBqp'cTcar&g*", ...) 

将生成相同的派生密钥字节 ( 17EB4014C8C461C300E9B61518B9A18B )。这些派生密钥冲突并不代表存在安全漏洞，因为仍然必须知道原始密码才能生成密码的哈希值。[11]利用这一性质，对于一些ZIP格式的加密压缩文件，可能存在两个可行的密码。[12][13]

PBKDF2 的一个缺点是，尽管可以通过改变迭代次数来任意调整所需的计算时间，但它可以用一个小电路和很少的RAM来实现，这使得使用特殊應用積體電路（ASIC）或图形处理器（GPU）进行暴力攻击相对低廉。[14]Bcrypt密码散列函数需要更大的RAM（但仍然不能单独调整，由给定的CPU时间决定）并且对此类攻击的抵抗力稍强， [15]而更现代的Scrypt密钥派生函数可以任意使用大量内存，因此更能抵抗ASIC和GPU攻击。[14]

2013年举行的密码哈希竞赛（PHC）鼓励开发一种更具抵抗力的密码哈希方法。2015年7月20日，Argon2被选为最终的获胜者，PHC还特别表彰了其他四种密码哈希方案：Catena、Lyra2、yescrypt和Makwa。[16]另一种替代方法是气球哈希，这是NIST密码指南中推荐的方法。[17]

• PBKDF2实现列表

• (PDF). RSA Laboratories. （原始内容 (PDF)存档于2017-04-11）.
• RFC 2898 – Specification of PKCS #5 v2.0.
• RFC 6070 – Test vectors for PBKDF2 with HMAC-SHA1.
• NIST Special Publication 800-132 Recommendation for Password-Based Key Derivation （页面存档备份，存于）