RC5
在密码学中,RC5是一种因简洁著称的对称分组加密算法。由罗纳德·李维斯特于1994年设计,[2]“RC”代表“Rivest Cipher”,或者“Ron's Code”(相较于RC2和RC4)。RC6算法是基于RC5的。
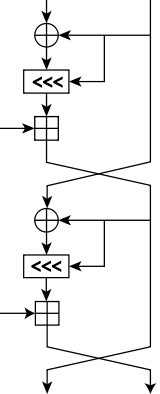 RC5分组密码的一轮(两个半轮) | |
| 概述 | |
|---|---|
| 设计者 | 罗纳德·李维斯特 |
| 首次发布 | 1994 |
| 继承算法 | RC6,Akelarre |
| 密码细节 | |
| 密钥长度 | 0至2040位(建议128位) |
| 分组长度 | 32,64或128位(建议64位) |
| 结构 | 类费斯妥网络 |
| 重复回数 | 1-255(原先建议12轮) |
| 最佳公开破解 | |
| 12轮RC5(64位块大小)可用244选择明文进行差分攻击。[1] | |
简介
和许多加密方法不同,RC5支持可变的块大小(32、64或128位元),密钥长度(0至2040位)和加密轮数(0~255)。最初建议选择的参数是64位的块大小,128位的密钥和12轮加密。
RC5的一个关键特征是使用基于数据的置换。RC5的其中一个目标是促进对于这类作为原始密码的操作的研究和评估。RC5也包括一些的取模加法和逻辑异或(XOR)运算。这个加密的一般结构是一种类费斯妥网络。加密和解密程序可以用几行代码写完,但密钥的生成算法更复杂。密钥扩展使用了e和黄金比例代入一个单向函数,将所得值作为“袖子里是空的”数字(即无任何来源依据的魔法数字)。算法的诱人的简洁性和基于数据的置换的特性,让RC5吸引了众多密码研究人员将其作为研究对象。 RC5通常被记为RC5-w/r/b,w=字的大小(以bit为单位),r=加密轮数,b=密钥的字节数。
算法
RC5加密和解密都将随机的密钥扩展成2(r+1)个字,在加密和解密的过程中,这些字将会被按顺序使用(而且每个字只使用一次)。以下的所有内容都来自Rivest的修订后的RC5的论文[3]
密钥扩展
密钥扩展算法将会在下面讲解,首先以伪代码表示,之后是用从参考资料中的论文附录中直接复制的C语言代码。
以下是论文中的命名方案,使用了这些变量名:
- w - 一个字的长度(以bit为单位),通常是16、32或64。加密以两个字为单位进行。
- u=w/8-一个字的长度,以字节为单位。
- b-密钥的长度,字节为单位。
- K[]-密钥,可以看作是一个由字节数据组成的数组(下标从0开始)。
- c - 密钥的长度,以字为单位(如果b=0,取1).
- L[] - 一个在密钥生成的临时数组,用来按字初始化密钥
- r - 加密的轮数。
- t=2(r+1) - 需要的轮加密的子密钥个数。
- S[] - 伪随机S数组。
- Pw - 第一个魔法数字,定义为 ,其中Odd取最接近给定输入的奇数,e 为自然对数的底数,w 见上述定义。对于常见的w值,对应的Pw 在这里以十六进制给出:
- 对于 w =16: 0xB7E1
- 对于 w =32: 0xB7E15163
- 对于 w =64: 0xB7E151628AED2A6B
- Qw -第二个魔法数字,定义为 其中Odd取最接近给定输入的奇数, 是黄金比例,w 见上述定义。对于共对于常见的w值,对应的Pw 在这里以十六进制给出:
- 对于 w =16:0x9E37
- 对于 w =32:0x9E3779B9
- 对于 w =64:0x9E3779B97F4A7C15
# Break K into words
# u = w / 8
c = ceiling( max(b, 1) / u )
# L is initially a c-length list of 0-valued w-length words
for i = b-1 down to 0 do:
L[i/u] = (L[i/u] << 8) + K[i]
# Initialize key-independent pseudorandom S array
# S is initially a t=2(r+1) length list of undefined w-length words
S[0] = P_w
for i = 1 to t-1 do:
S[i] = S[i-1] + Q_w
# The main key scheduling loop
i = j = 0
A = B = 0
do 3 * max(t, c) times:
A = S[i] = (S[i] + A + B) <<< 3
B = L[j] = (L[j] + A + B) <<< (A + B)
i = (i + 1) % t
j = (j + 1) % c
# return S实例源码由Rivest的RC5论文的附录提供。这个代码实现对应 w = 32, r = 12, b = 16。
void RC5_SETUP(unsigned char *K)
{
// w = 32, r = 12, b = 16
// c = max(1, ceil(8 * b/w))
// t = 2 * (r+1)
WORD i, j, k, u = w/8, A, B, L[c];
for(i = b-1, L[c-1] = 0; i != -1; i--)
L[i/u] = (L[i/u] << 8) + K[i];
for(S[0] = P, i = 1; i < t; i++)
S[i] = S[i-1] + Q;
for(A = B = i = j = k = 0; k < 3 * t; k++, i = (i+1) % t, j = (j+1) % c)
{
A = S[i] = ROTL(S[i] + (A + B), 3);
B = L[j] = ROTL(L[j] + (A + B), (A + B));
}
}
加密
加密涉及的一个简单的函数的几轮加密。基于安全需要和时间方面的考虑,12或20轮是建议的值。除了上述使用的变量,以下变量在算法之中使用:
- A,B - 要加密的明文的两个字。
A = A + S[0]
B = B + S[1]
for i = 1 to r do:
A = ((A ^ B) <<< B) + S[2 * i]
B = ((B ^ A) <<< A) + S[2 * i + 1]
# The ciphertext block consists of the two-word wide block composed of A and B, in that order.
return A, B
Rivest给出的示例C源码如下
void RC5_ENCRYPT(WORD *pt, WORD *ct)
{
WORD i, A = pt[0] + S[0], B = pt[1] + S[1];
for(i = 1; i <= r; i++)
{
A = ROTL(A ^ B, B) + S[2*i];
B = ROTL(B ^ A, A) + S[2*i + 1];
}
ct[0] = A; ct[1] = B;
}
解密
解密实际上就是直接把加密过程颠倒。以下代码展示了这个过程。
for i = r down to 1 do:
B = ((B - S[2 * i + 1]) >>> A) ^ A
A = ((A - S[2 * i]) >>> B) ^ B
B = B - S[1]
A = A - S[0]
return A, B
Rivest给出的示例C源码如下。
void RC5_DECRYPT(WORD *ct, WORD *pt)
{
WORD i, B=ct[1], A=ct[0];
for(i = r; i > 0; i--)
{
B = ROTR(B - S[2*i + 1], A) ^ A;
A = ROTR(A - S[2*i], B) ^ B;
}
pt[1] = B - S[1]; pt[0] = A - S[0];
}
密码分析
12轮RC5(64位块)容易受到使用了244的选定的明文的差分攻击。[1] 18–20轮加密则被认为可以提供足够的保护。
拥有其算法专利的公司RSA安全,[4] 提供一系列的10,000美元的奖金作为破译用RC5加密的密文的奖励,但这些竞赛已经在2007年5月停止。其中的一部分已经在Distributed.net组织下利用分布式计算破解。Distributed.net暴力破解了用56位和64位密钥的RC5加密的密文,正在尝试破解72位密钥的密文;截至2018年2月,5.02%的密钥空间已被遍历。以目前的速度,这将需要大约166年以测试的每一个可能的剩余密钥,以此才能保证项目的完成。[5]这项任务启发了许多在集群计算领域的新兴的开发研究。[6]
参见
- Madryga
- Red Pike
参考资料
- Biryukov A.和Kushilevitz E.(1998年)。改进的密码分析的RC5的。EUROCRYPT1998年。
- Rivest, R. L. (pdf). : 86–96. 1994 [2018-10-02]. (原始内容存档 (PDF)于2007-04-17).
- (PDF). [2018-09-27]. (原始内容存档 (PDF)于2018-09-21).
- Rivest, R. L, "Block Encryption Algorithm With Data Dependent Rotation", 美國專利第5,724,428号, issued on 3 March 1998.
- . [2018-09-27]. (原始内容存档于2018-10-09).
- . [2014-10-28]. (原始内容存档于2014-10-28).