三相 (电学)
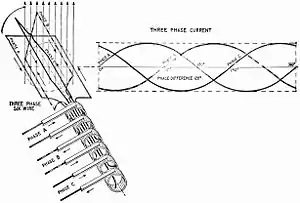
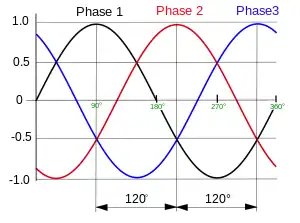
在电子工程学中,三相交流电一般是将可变的电压通过三组不同的导体。这三组电压幅值相等、频率相等、彼此之间的相位差为120度。
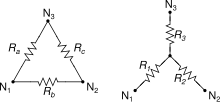
通常来说,三相交流电分三角形接法(Δ)和星型接法(Y)两种。三角形接法即为将各相电源或负载依次首尾相连,形成一个三角环;而星型接法则是将各相电源或负载的一端连接在一点,形成一个中性点,这种接法又称为三相三线制。如果从该中性点再引出一条中性线,则整个结构变为三相四线制。其中星型接法允许对各相加上不同的电压。例如常见的230/400伏三相交流电,就是在中性点和任意一相上加上230伏,余下的两相各加上400伏的电压。三角形接法由于各相首尾相连,只能存在一种电压,但是其优点在于即使三相中有一相失去作用,整个系统仍然可以运作(效率为原来的57.7%)。[1]
電壓和電流
線電壓(Line to Line Voltage, Line Voltage)為兩條相線間的電壓。相電壓(Vph)為負載端所獲得的電壓,隨連接方式而異。
線電流(IL)為相線上的電流大小。相電流(Iph)為負載端的電流大小。
- 星形接法
在星形接法,线電壓是相電壓的√3倍,線電流等於相電流。
- 三角形接法
在三角形接法,线電壓等於相電壓,线電流是相電流的√3倍。
功率
星形接法和三角形接法的總功率,都可使用同一公式計算:
- 開三角形接法
三角形接法其中一個繞阻被移除,則變成開三角形(Open Delta)。
假設單相變壓器可以輸出電壓V及電流I,兩個變壓器的功率為
用作三相變壓器時,功率為
換言之,兩個變壓器可使用的功率為原來的86.6%。
對比三個變㱘器,整個系統的功率變成原來的57.7%。因為兩個變壓器的功率因素不同,其中一個提供无功功率,另一個消耗无功功率,所以可用輸出並不是66.7%。
稳定输出


一般在三相的电力系统中,每一相负载的做功的大小均相同。通常会先论证电动机在稳定输出的情况下运作,再考虑不稳定的情况。
恒定功率转化
三相发电机的特性在于,当各相的负载具有电阻性质时,其输出功率是恒定的。
为了使计算更方便,先定义一个无量纲的功率值作为中间量,则:
代回:
最终结果中不含(相位角)由此可见发电机动率的输出不会随着时间的变化而变化。对于大型发电机来说,这点尤为重要。
实际上,发电机的负载不一定要带有电阻的性质,只需各个相位相等即可,设:
因此最大电流为:
所有相位上的瞬时电流大小为:
这时各个相位的功率输出为:
利用三角恒等式里的积化和差与和差化积公式:
得出瞬时功率输出为:
中括号中的三项互相抵消,得出最终的结果为:
或者
中線電流
当一个星形接法是平衡負載,即使接上中線也沒有電流。流过中性点的电流即三相电流的向量之和,参见基尔霍夫定律。
定义一个非无量纲量的电流,大小为:
流过中線的电流大小为零。因此将中線拿掉而不影响电路本身,证明输出的功率是恒定的。一般三相三線制只有在三相的电源或者负荷都连接在同一个电路上(例如三相电动机),否则各相的输入电压的波动会造成输出功率的不稳定。
不稳定输出
在实际的应用中,很少出现理论上输出功率很稳定的情况。利用对称分量法来简化电路,一个不恒定输出的系统可以看作是三个电压分别为正、零、负的恒定输出系统的叠加。
在一个限定的三相电路中,只需要知道三相的模量和流过中性点电流的大小。中性点电流的计算一般先求三相电流的复数之和,在代换回极坐标系的形式。假设三相内的电流分别为, 和,则流经中性点的电流大小为:
最后的极坐标系中的三相和的模量:
旋转磁场
任何一个多相的电路,根据电流随着时间的变化,通过旋转即可生成磁场,这也是异步电动机的工作原理。感应电动机是异步电动机的一种,指的是仅有一套绕组联接电源的异步电动机。
励磁磁动势
定子三相对称绕组流过三相对称电流时,产生合成基波旋转磁动势。将该磁动势用空间矢量F0表示,其幅值为
式中,N1和kdp1分别为定子绕组的每相串联匝数和基波绕组因数;p为极对数;m1为定子绕组相数,对于三相异步电动机,m1=3。
对于其他多相系统的转化
任意两个随着时间t变化的电压之间一定存在着相互位移的关系,同样,一个三相的电源通过变压器可以转化为多相。例如,利用特殊的变压器,能将三相的电源转变为一个二相电源。此类变压器一般称为相位转换器。当三相的电力通过高压线传输到用户的社区在传输到每一户家中时,一般利用角接电容或星接电容将三相变为单项,为家庭用户提供电力。但是相应的,输出功率会有所下降。[5]
输出功率的测量
用传感器可以测量三相电路的输出功率,无中线要用到两个传感器,有中性线要用到三个。[6]需要使用传感器的数量总是比测量的电路的数量少一个。[7]若採用高壓計量,則需要兩個电压互感器及兩個电流互感器(2VT+2CT)分別用來量度電壓及電流。
若使用功率分析儀用來分析諧波電流,宜使用四個电流互感器測量所有帶電導體的電流,以提高準確度。因為每個电流互感器都有誤差,利有三個測量值計算剩下的未知值,誤差也變成了三倍。
参考资料
- http://www.ibiblio.org/kuphaldt/socratic/output/deltawye_instructor.pdf (页面存档备份,存于) public domain
- Keljik, Jeffrey. . Clifton Park, NY: Cengage Learning/Delmar. 2008: 49. ISBN 1435400291.
- Lowenstein, Michael. . IAEI Magazine. [24 November 2012]. (原始内容存档于2011年3月27日).
- Enjeti, Prasad. (PDF). Texas A&M University Power Electronics and Power Quality Laboratory. [24 November 2012]. (原始内容存档 (PDF)于2010-06-13).
- . [2013-07-15]. (原始内容存档于2021-03-24).
- (PDF). [2013-07-15]. (原始内容 (PDF)存档于2020-07-03).
- (PDF). [2013-07-15]. (原始内容 (PDF)存档于2013-03-19).