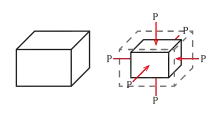
体积模量
定义
体积模量可由下式定义:
其中为压強, 为体积, 是压強对体积的偏导数。体积模量的倒数即为一种物质的压缩率。
还有其他一些描述材料对应变的反应的物理量。譬如剪切模量描述了材料对剪切应变的反应;而杨氏模量则描述了材料对线性应变的反应。对流体而言,只有体积模量具有意义。而对于不具有各向同性的固体材料(如纸、木等),上述三种弹性模量则不足以描述这些材料对应变的反应。
热力学关系
严格的说,体积模量是一个热力学量。说明在何种温度变化条件下对体积模量是有必要的。等温体积模量()以及定熵(绝热)体积模量()或其他形式都是可能出现的。实践中上述区分只是用于对气体的讨论中。
对于理想氣體,绝热体积模量 為:
而等温体积模量 為:
其中 为绝热指数; 为压强。
对于流体,体积模量和密度决定了在该种材料中的音速。此种关系由下式说明:
固体可以传递横波,故要决定固体中的声速还需要其他的弹性模量,如剪切模量。
部分材料的体积模量
| 材料 | 体积模量(Pa) |
|---|---|
| 玻璃 | 3.7×1010[1] |
| 钢 | 16×1010[1] |
| 水银 | 2.5×1010[1] |
| 乙醇 | 0.09×1010[1] |
| 金刚石 | 442×109[2] |
| 水 | 2.2×109[3] |
| 空气 | 1.42×105 绝热体积模量 |
| 空气 | 1.01×105 等温体积模量 |
| 固态氦 | 5×107 (估计值)[4] |
参考文献
- 钟锡华、周岳明. . 北京大学出版社. 2000年12月: 204. ISBN 978-7-301-04591-6.
- Phys. Rev. B 32, 7988 - 7991 (1985), Calculation of bulk moduli of diamond and zinc-blende solids
- . [2010-07-28]. (原始内容存档于2012-08-30).
- http://www3.interscience.wiley.com/cgi-bin/abstract/105558571/ABSTRACT%5B%5D
| 换算公式 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 均质各向同性线弹性材料具有独特的弹性性质,因此知道弹性模量中的任意两种,就可由下列换算公式求出其他所有的弹性模量。 | ||||||||||
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.