全內反射
全內反射(英語:),又稱,是一種光學現象。當光線經過兩個不同折射率的介質時,部份的光線會於介質的界面被折射,其餘的則被反射。但是,當入射角比臨界角大時(光線遠離法线),光線會停止進入另一介面,全部向內面反射。[1] [2]


這只會發生在當光線從光密介質(較高折射率的介質)進入到光疏介質(較低折射率的介質),入射角大於臨界角(critical angle)時。因為沒有折射(折射光線消失)而都是反射,故稱之為全內反射。例如當光線從玻璃進入空氣時會發生,但當光線從空氣進入玻璃則不會。最常見的是沸騰的水中氣泡顯得十分明亮,就是因爲發生了全內反射。
克卜勒(,1571-1630)在西元1611年於他的著作《》中,已發表全内反射的現象。
光學描述
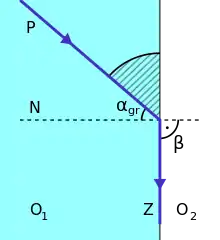
如图一所示: 光线从折射率较高的 介质进入折射率较低的 介质: 当入射角 即少於临界角 时,光线同时发生趨離 介质(normal)的折射,以及向 介质的反射(图一中红色光线所示); 当入射角 即大於临界角 时, 介折射的光线消失,所有光线向 介质中(英語:)反射(图一中蓝色光线所示); 全内反射仅仅可能发生在当光线从较高折射率的介质(也称为光密介质)进入到较低折射率的介质(也称为光疏介质)的情况下,例如当光线从玻璃进入空气时会发生,但当光线从空气进入玻璃则不会。
例如:
- 為光纖核心折射率 (英語:) 1.5
- 為空氣折射率 (英語:) = 1
- =
- =未知
那麼空氣和光纖核心临界角( )為
临界角
临界角(英語:)是使得全内反射发生的最少的入射角。入射角是从折射界面的法线量度计算的。临界角()可從以下方程式計算[2][4]:
其中是较低密度介质的折射率,及是较高密度介质的折射率。这条方程式是一条斯涅尔定律的简单应用,当中折射角为90°。 当入射光线是准确地等于临界角,折射光线会循折射界面的切线进行。以可见光由玻璃进入空气(或真空)为例,临界角约为48.7°。
受抑全内反射技術
如果,我們取兩個密介質區域,中間夾著一薄層的疏介質,例如一層厚度與入射光波波長大小相當的空氣薄層,讓光束透過自密介質區射向空氣層,則光會透過薄層,再進入對向的密介質區。這種入射角大於臨界角 ,而又能超越障礙,透射到另一介質的現象,稱為受抑全内反射(Frustrated Total Reflection)。[5]
這種現象的產生是由於當發生全反射時,電磁場並非完全沒有進入疏介質;只是進入疏介質區域的電磁場強度以指數式衰減的形式消失。所以在全反射的狀態之下,仍然有部分電磁場進入疏介質薄層後再進入對向的密介質區,只不過這種電磁波的強度會隨著光波行進距離越遠而很快耗損殆盡。[5]
應用

光導纖維就是利用了全内反射這一原理,由於反射時沒有光線的損失,因此信號可以傳輸到極遠的距離,廣泛應用於內視鏡及電信上。海市蜃樓亦是由此一原理所生成,光線從較密的介質(冷空氣)進入到較疏的介質(近地面的熱空氣)。
參考文獻
- Hecht, Eugene. 4th. United States of America: Addison Wesley. 2002. ISBN 0-8053-8566-5 (英语).
- Paul Lorrain; Dale P. Corson. 3rd. New York: W. H. Freeman and Company. 1988: 581. ISBN 0-7167-1869-3 (英语).
- . labman.phys.utk.edu. [2020-05-09]. (原始内容存档于2020-10-22).
- John R. Reitz; Frederick J. Milford. . Fourth. Addison-Wesley Publishing Company. 1993: 454. ISBN 0-201-52624-7 (英语).
- 李, 怡嚴. . 4 12th. 台北市: 台灣東華書局股份有限公司. 1988: 1461 (中文(臺灣)).