取整函数
在数学和计算机科学中,取整函数是一类将实数映射到相近的整数的函数。[1]

下取整函数
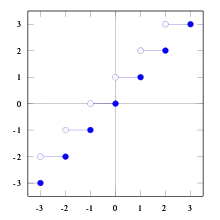
上取整函数
常用的取整函数有两个,分别是下取整函数(英語:)和上取整函数()。
下取整函数即為取底符號,在数学中一般记作或者或者,在计算机科学中一般记作floor(x),表示不超过x的整数中最大的一个。
举例来说,,,,。对于非负的实数,其下取整函数的值一般叫做它的整数部分或取整部分。而叫做x的小数部分。每个分数都可以表示成其整数部分与一个真分数的和,而实数的整数部分和小数部分是与此概念相应的拓延。
下取整函数的符号用方括号表示(),称作高斯符号,首次出現是在卡爾·弗里德里希·高斯的數學著作《算术研究》。
上取整函数即為取頂符號在数学中一般记作,在计算机科学中一般记作ceil(x),表示不小于x的整数中最小的一个。
举例来说,,,,。
计算机中的上取整函数和下取整函数的命名来自于英文的ceiling(天花板)和floor(地板),1962年由肯尼斯·艾佛森于《A Programming Language》引入。[2]
性质
对于高斯符號,有如下性质。
- 按定义:
- 当且仅当x为整数时取等号。
- 设x和n为正实数,则:
- 当n为正整数时,有:
- 其中表示除以的餘數。
- 对任意的整数k和任意实数x,
- 一般的數值修約規則可以表述为将x映射到floor(x + 0.5);
- 高斯符號不是连续函数,但是上半连续的。作为一个分段的常数函数,在其导数有定义的地方,高斯符號导数为零。
- 设x为一个实数,n为整数,则由定义,n ≤ x当且仅当n ≤ floor(x)。
- 當x是正數時,有:
- 用高斯符號可以写出若干个素数公式,但没有什么实际价值,見§ 質數公式。
- 对于非整数的x,高斯符號有如下的傅里叶级数展开:
- 根据Beatty定理,每个正无理数都可以通过高斯符號制造出一个整数集的分划。
- 最后,对于每个正整数k,其在 p 进制下的表示有 个数位。
函數間之關係
由上下取整函數的定義,可見
等號當且僅當為整數,即
實際上,上取整與下取整函數作用於整數,效果等同恆等函數:
自變量加負號,相當於將上取整與下取整互換,外面再加負號,即:
且:
至於小數部分,自變量取相反數會使小數部分變成關於1的「補數」:
上取整、下取整、小數部分皆為冪等函數,即函數疊代兩次的結果等於自身:
而多個上取整與下取整依次疊代的效果,相當於最內層一個:
因為外層取整函數實際衹作用在整數上,不帶來變化。
應用
参考来源
- Ronald Graham, Donald Knuth and Oren Patashnik. "Concrete Mathematics". Addison-Wesley, 1999. Chapter 3, "Integer Functions".
- Iverson, Kenneth E. . Wiley. 1962.
- Graham, Knuth & Patashnik 1994,第73頁.
- Graham, Knuth & Patashnik 1994,第85頁.
- Graham, Knuth & Patashnik 1994,p. 85 and Ex. 3.15.
- Graham, Knuth & Patashnik 1994,Ex. 3.12.
- Graham, Knuth & Patashnik 1994,第94頁.
- Lemmermeyer 2000,§ 1.4, Ex. 1.32–1.33.
- Hardy & Wright 1980,§§ 6.11–6.13.
- Lemmermeyer 2000,第25頁.
- Crandall & Pomerance 2001,Ex. 1.3, p. 46,求和式的上限可以換成。尚有一個等價的表述:為質數當且僅當
- Hardy & Wright 1980,§ 22.3.
- Ribenboim 1996,第186頁
- Ribenboim 1996,第181頁.
- Crandall & Pomerance 2001,Ex. 1.4, p. 46.
- Ribenboim 1996,第180頁(譯文):「雖然該些公式毫不實用⋯⋯但邏輯學家希望清晰明白不同公理體系,如何推導出算術各方面,則或許與此有關⋯⋯」
- Hardy & Wright 1980,第344—345頁(譯文):「若數的準確值⋯⋯可以無關質數的方式表達,則該些公式之任一(或一切類似公式)的地位將截然不同。似乎沒有此種可能,但卻不能完全排除。」
- Crandall, Richard; Pomerance, Carl. . New York: Springer. 2001 [2022-02-06]. ISBN 0-387-94777-9. (原始内容存档于2022-04-09).
- Graham, Ronald L.; Knuth, Donald E.; Patashnik, Oren. . Reading Ma.: Addison-Wesley. 1994. ISBN 0-201-55802-5.
- Hardy, G. H.; Wright, E. M. . Oxford: Oxford University Press. 1980. ISBN 978-0-19-853171-5.
- Lemmermeyer, Franz. . Berlin: Springer. 2000. ISBN 3-540-66957-4.
- Ribenboim, Paulo. . New York: Springer. 1996. ISBN 0-387-94457-5.
另见
截尾函数
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.