除法
数学中,尤其是在基本计算裏,除法可以看成是「乘法的反运算」,也可以理解为「重复的减法」。除法运算的本质就是「把参与运算的除数变为,得出同比的被除数的值」。
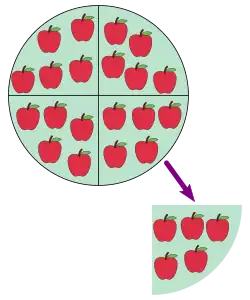
將20個蘋果平均分成四等分(左上),每份有5個蘋果(右下),即;亦可以說成,將20個蘋果每5個分成一份(右下),共可分成四等分(左上),此時可以表達為
| 算术运算 | ||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||
例如:,就好像, ,被減了兩次後,就變成了。
如果
而且不等于零,那么
其中,a称为商数,b称为除数,c称为被除数。
如果除式的商數()必須是整數,则称为带餘除法,与相差的数值,称为餘數()。
這也意味著
在高等数学(包括在科学与工程学中)和计算机编程语言中,写成。如果我们不需要知道确切值或者留待以后引用,这种形式也常常是称之为分数的最终形式。其中尋找商數的函數為,尋找餘數的函數則為。
整除
整除是数学中两个自然数之间的一种关系。自然数可以被自然数整除,是指是的因數,且a是b的整数倍数,也就是除以没有餘数。
因數判別法可參照整除規則。
表示法
表示整除,即是的倍数,是的因数。
举例
可以被整除,记作。
不能被整除(因为餘数为),记作。在上加一条斜线即表示不整除。
除法计算
根据乘法表,两个整数可以用长除法(直式除法)笔算。如果被除数有分数部分(或者说时小数点),计算时将小数点带下来就可以;如果除数有小数点,将除数与被除数的小数点同时移位,直到除数没有小数点。
算盘也可以做除法运算。
多項式的除法
和整数之间的带余除法类似,一元多项式之间也可以进行带余除法。可以证明,设有多项式和非零多项式,则存在唯一的多项式和,满足:
而多项式若非零多项式,則其冪次严格小于的冪次。
作为特例,如果要计算某个多项式除以一次多项式得到的餘多项式,可以直接将代入到多项式中。除以的餘多项式是。
具体的计算可以使用类似直式除法的方式。例如,计算除以,列式如下:
因此,商式是,餘式是。
重要性質
通常不定义除以零这种形式。亦即當除以0 或分數的分母為0 時,該式或該數無意義。
参见
- 筹算除法
- 同餘
- 余数
- 带餘除法
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.
