星盘
星盤(古希臘語: ; 阿拉伯语: ; 波斯語: )是一種古老的天文儀器,可以说是手持的宇宙模型。它的各種功能也使它成為一個精巧的測斜儀和一個能够解决天文學中幾種問題的類比計算裝置。在最簡單的形式中,它是一個金屬圓盤,帶有導線、切口和穿孔的圖案,允許使用者精確計算天體的位置。歷史上的天文學家使用它,無論在白天或夜晚,能够量測天體在地平線上的高度;它可以用於識別恆星或行星,確定給定當地時間的當地緯度(反之亦然),量測或進行三角測量。它在古典時代、伊斯蘭黃金時代、歐洲中世紀和地理大發現時代中,用於所有這些目的。




星盤的重要性不僅來自於天文學研究的早期發展[1],對於確定陸地或平靜海面上的緯度也很有效。然而,在波濤洶湧的海面上,船舶的甲板隨之升降時就不太可靠,為了解决這個問題,於是開發出了水手星盤。
應用

一位10世紀的天文學家推斷,星盤的各種功能大約有1000種應用[3],範圍從占星術、天文學和宗教,到季節和日常計時和潮汐表。在星盤被大量使用的時代,占星術被廣泛認為與天文學一樣是一門嚴肅的科學,對兩者的研究是並行不悖,齊頭並進的。天文學的興趣在民間天文學(阿拉伯的前伊斯蘭傳統),和數學天文學之間有所不同,民間天文學與天文和季節性觀測有關,數學天文學則為知識實踐和基於天文觀測的精確計算提供資訊。關於星盤的宗教功能,伊斯蘭祈禱時間的要求是由天文數值確定,以確保每天的精確時間,穆斯林祈禱和朝拜必須朝向麥加的方向,也可以通過星盤這種裝置確定。除此之外,由星盤計算得出的陰曆對伊斯蘭教具有重要意義,因為它决定了重要宗教儀式的日期,如齋戒月。
詞源
《牛津英語詞典》給出了英語單詞"astrolabe"翻譯自"star-taker",並通過中世紀拉丁語將其追溯到Greek字詞"ἀστρολάβος": [4][5],來自 "star"和λαμβάνειν : "to take"[6]。
在中世紀伊斯蘭世界的阿拉伯語單詞(即星盤)被賦予了各種詞源。
在阿拉伯文中,這個詞被從希臘單詞直接翻譯成"星星塔"(阿拉伯语:,"star-taker")[7]。
比魯尼引用並責備中世紀科學家哈姆扎伊斯法哈尼,他說[7]:"asturlab是這個波斯語短語的阿拉伯化"(,意思是"星星的接受者"。)[8]。在伊斯蘭黃金時代的來源,還有一個民間詞源這個詞作為"lines of lab",其中"Lab" 指的是伊德里斯(以諾)的某個兒子。 10世紀的一位名叫阿裡·伊本·易卜拉欣·庫米的科學家提到了這個詞源,但被花拉子米拒絕了[9]。
历史

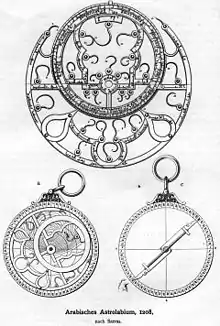
古代的星盘
早期的星盤是佩爾加的阿波羅尼奧斯在西元前220年至150年之間在希臘化時代發明的,但一般都認為是喜帕恰斯發明的。星盤是平面球和望筒的結合,實際上是一個類比計算機,能够解决天文學中的幾種不同問題。亞歷山大的席恩(约 335–约 405)寫了一篇關於星盤的詳細論文,路易斯[10]認為托勒密使用星盤進行了占星四書中記錄的天文觀測。平面星盤的發明有時被錯誤地歸因於席恩的女兒希帕提亞(约350–370; died 415 AD)[11][12][13][14]。但事實上,在希帕提亞出生之前至少500年,星盤已經在使用了[12][13][14]。這個錯誤歸因來自於希帕提亞的學生辛奈西斯(约373 – 约414)[12][13][14],其中提到希帕提亞教他如何建造平面星盤,但並沒有任何文字提到是她自己發明了它[12][13][14]。
星盤在整個拜占庭時期提的希臘語世界中一直在使用。大約在西元550年,基督教哲學家約翰·費羅普勒斯用希臘語寫了一篇關於星盤的論文,這是現存最早的關於該儀器的論文[lower-alpha 1]。美索不達米亞主教西弗勒斯·塞博赫特也在7世紀中葉用敘利亞語寫了一篇關於星盤的論文[lower-alpha 2]塞博赫特在他的論文中提到星盤是由黃銅製成的,這表明金屬星盤在東正教的發展,早於伊斯蘭世界或拉丁西方發展之前就已經為人所知[15]。
文藝復興時期最早涉及科學問題的論文多基於早期的古典作品,並且經常關注托勒密教義。
中世紀時代
星盤在中世紀伊斯蘭世界得到進一步發展,其中穆斯林天文學家在設計中引入了角度的尺度[16],在地平線上添加標示方位的圓[17]。它在整個穆斯林世界被廣泛使用,主要是作為一種導航和一種尋找朝拜,即麥加方向的管道。八世紀的數學家穆罕默德·法紮裏是伊斯蘭世界製作星盤的第一人[18]。
數學背景是由穆斯林天文學家巴塔尼在其論文《Kitab az Zij》(約西元920年)中建立的,該論文由柏拉圖·提布提努斯(De Motu Stellarum)翻譯成拉丁文。現存最早的星盤日期為伊斯蘭曆315(西元927-28年)。在伊斯蘭世界,星盤被用來確定日出和恆星升起的時間,以幫助安排晨禱(salat)。在10世紀,阿左飛首先描述了星盤的1,000多種不同用途,包括天文學、占星術、導航、測量學、計時、祈禱、晨禱、基卜拉等領域[19][20]。
球面星盤是星盤和渾儀的變體,是由天文學家和伊斯蘭世界的發明家在中世紀發明的[lower-alpha 3]。 對球面星盤的描述,最早可以追溯到Al Nayrizi([floruit | fl.]892-902)。在12世紀,薩拉夫·丁·圖西發明了"線性星盤",有時被稱為"圖西尺規"。這是"一根簡單的木棒,有刻度標記,但沒有瞄準鏡。它配有鉛垂線和雙弦,用於進行角度量測,並帶有穿孔指針"[21]。齒輪機械星盤是由伊斯法罕的Abi Bakr於1235年發明的[22]。
西歐第一個已知的金屬星盤是11世紀在葡萄牙用黃銅製成的德東布(英語:)星盤[23][24]。金屬星盤避免了大型木製星盤容易出現的翹曲,因此可以建造更大、更精確的儀器。但金屬星盤比同樣大小的木製星盤重,因此很難在航海中使用[25]。
Reichenau Abbey的Herman Contractus研究了11世紀"量測天文學"中星盤的使用[26]。馬里孔特的彼得在13世紀後半葉寫了一篇關於全球星盤的構造和使用的論文,題為"Nova compositio astrolabii Specialis"。可以在牛津科學史博物館找到全球星盤。[27]。伊斯蘭儀器歷史學家大衛·A·金(英語:)將阿勒坡的伊本·薩拉吉(英語:,又名Ahmad bin Abi-Bakr;fl.1328)設計的全球星盤描述為"整個中世紀和文藝復興時期最複雜的天文儀器"[28]。
英國作家傑弗里·喬叟(約1343-1400)主要基於馬沙拉或ibn al-Saffar的作品,為他的兒子編纂了《"星盤論"》[29][30]。法國天文學家和占星家Pélerin de Prusse等人也翻譯同一來源的著作。關於星盤的第一本印刷書籍是普拉查提斯的克利斯蒂安的《星盤的組成和使用》,也使用了馬沙拉的資料,但相對來說是原創的。
在1370年,印度第一篇關於星盤的論文是由耆那教天文學家Mahendra Suri撰寫的,標題為"Yantrarāja"[31]。
水手們在出海時使用一種簡化的星盤,稱為"balesilha",以獲得準確的緯度讀數。"balesilha"是由亨利王子(1394-1460)在前往葡萄牙的途中推廣的[32]。
幾乎可以肯定的是,奧里拉克的格伯特(Gerbert d'Aurillac)(後來的教宗思維二世)首先將星盤帶到比利牛斯山脈北部,在11世紀初的某個時候,它在法國蘭斯的學校被綜合到四藝中[33]。 在15世紀,法國儀器製造商Jean Fusoris(約1365-1436年)也開始在他位於巴黎的商店裡重新製作和銷售星盤,以及可擕式日晷和其他當時流行的科學設備;他的星盤至今仍然留存了13個[34]。15世紀早期,歐洲工藝的另一個特殊例子是安東尼烏斯·德·帕森托設計的星盤,由多明尼克斯·德·蘭紮諾製造,日期為1420年[35]。
在16世紀,Johannes Stöffler出版了《"Declicatio fabricae ususque astrolabii"》,這是一本星盤構造和使用手册。由Georg Hartmann製作的四個相同的16世紀星盤,為分工的批式生產提供了一些最早的證據。
中国的星盘
用於中國的星盤,跟西方不一樣的地方是中國使用的是12個時辰,分別是子時、丑時、寅時、卯時、辰時、巳時、午時、未時、申時、酉時、戌時、亥時,依照上面的順序排版。
構造
星盤由一個稱為"母盤"(mater)的圓盤組成,其深度足以容納一個或多個稱為"子盤"或"克利莫"的平板。一個子盤是為一個特定的緯度製作的,上面刻著一個圓的球極平面投影,表示天球在地平線上部分的方位角和高度角。母盤金屬邊緣通常分為時間、弧度,或兩者並存[39]。
在母盤和子盤上方,是一個"網"的框架,承載著黃道平面的投影和幾個指針,可以自由旋轉來指示最亮恆星的位置。這些指針取決於工匠的技能,通常只是簡單的點,但也可以是非常精細和藝術化。有一些星盤的例子,其中有球、星星、蛇、手、狗頭和樹葉等形狀的藝術指針[39]。標示的恆星名稱通常用阿拉伯語或拉丁語刻在指針上[40]。一些星盤有一個狹窄的"尺子"或"標籤",可以在網上旋轉,並且用赤緯的刻度來標記。
代表天空的網,起著星圖的作用。當它旋轉時,恆星和黃道在子盤上的座標投影上移動。一個完整的旋轉相當於一天的過去。因此,星盤是現代星座盤的前身。
在母體的背面,通常刻有許多刻度,這些刻度在星盤的各種應用中都很有用。但這些刻度會因為設計師不同而有很大的差異,可能包括時間轉換曲線、將一個月中的某一天轉換為太陽在黃道上位置的日曆、三角尺度以及圍繞後緣周圍360度的刻度。"照準儀"則附在背面。當星盤垂直握持時,可以旋轉星盤,並以方位儀觀察太陽或恆星,以便可以從星盤的刻度邊緣讀取(“得到”)其高度(以度為單位);因此,這個詞的希臘語詞根:「astron」(ἄστρον)=star+“lab-”(λαβ-)=得到(to take)。
一些星盤的背面也出現一個可以產生陰影的正方形,這種星盤是穆斯林占星家在9世紀開發的,而古希臘傳統的設備背面只有高度的刻度[41]。這被用來轉換陰影長度和太陽的高度,其用途多種多樣,從可以量測到量測無法到達之處的高度[42]。
星盤製造商通常會在設備的背面署名,並在星盤背面刻有銘文。如果有該物品的贊助人,則其名稱會出現在正面;或者在某些情况下,在位蘇丹或星盤師的姓名也會出現在此處[43]。星盤的製造日期經常也會被簽署,這使歷史學家能够確定這些裝置是世界上第二古老的科學儀器。 星盤上的銘文也讓歷史學家得出結論,天文學家傾向於自己製作星盤,但許多星盤也是按訂單製作的,並有庫存出售,這表明這些設備在當代有一定的市場[43]。
星盤的一部分由一個圓盤、一個瞄準管、一個照準儀和裝有刻度尺的臂組成。圓形圓盤是星盤的主要部分,它主要用於查看天空中的物體。瞄準管放置在圓盤的頂部,用於觀察恆星或行星。照準儀有垂直和水平的十字準線,在稱為等高圈(almucantar)的方位環上繪製位置。一個稱為幅的臂從星盤的中心連接到光軸,光軸與另一個包含高度和距離測量值刻度的臂(也稱為幅)平行。
數學基礎
星盤的建造和設計是基於天球的立體投影的應用。通常進行投影的點是南極,投影到的平面是赤道的平面[44]。
通過立體投影設計鼓室
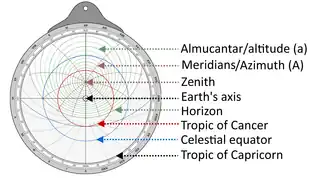
鼓室捕捉到天球坐標軸,「地球」將在這些坐標軸上旋轉。它是能够在日和年的特定時間點上精確確定恆星位置的部件。
因此,它應該投影:
回歸線和赤道定義了鼓室

在影像的右側:
- :淺藍色的球體代表天球。
- :藍色箭頭表示正北(北極星)的方向。
- :中心的藍色點代表地球(觀測者的位置)。
- :天球的地理南面是投影極。
- :赤道平面做為投影平面。
- 三個平行的圓圈代表地球主緯度圈在天空中的投影:
當投影到赤道平面上時,三個同心圓對應於地球的三個緯度圈(影像的左側)。其中最大的一個是南回歸線,它定義了星盤的鼓室大小。鼓室的中心(以及三個圓的中心)實際上是地球自轉的南北軸,因此,隨著時間的推移,星盤的「中心」將圍繞這一點旋轉(由於地球自轉)。
鼓室上的三個同心圓有助於確定全年至日和分日的確切時刻:如果知道太陽在「日期」上的位置,並且它的位置及鼓室的外圓(南回歸線)重合,它象徵著冬至(對於南回歸線的觀測者來說,太陽將處於天頂,意味著南半球的夏天和北半球的冬天)。另一方面,如果它的位置與內圈(北迴歸線)重合,則表示夏至。如果它的位置在中間的圓(赤道)上,它對應於兩個分點中的一個。
地平線和高度量測

在第一個影像的右側:
- :藍色箭頭表示正北(北極星)的方向。
- :中心的藍色點代表地球(觀測者的位置)。
- :黑色箭頭代表觀測者的天頂方向(根據觀測者緯度的不同而變化)。
- :黑圈代表觀測者周圍的地平線,它垂直於天頂向量,定義了觀測者可見的天球部分。
- :天球的地理南面是投影極。
- :赤道平面做為投影平面。

當將地平線投影到赤道平面上時,它會轉化為相對於南北軸(鼓室中心)向上移動的橢圓。這意味著天球的一部分將落在鼓室的外圓(南回歸線)之外,因此不會被呈現。
此外,當繪製平行於地平線直到天頂的圓(地平緯圈)時,會構建一個連續橢圓的網格,當「基準」與設計的鼓室重疊時(如第二張影像所示),可以確定恆星的高度
子午線與方位量測

在影像右側:
- :藍色箭頭表示正北(北極星)的方向。
- :中心的藍色點代表地球(觀測者的位置)。
- :黑色箭頭代表觀測者的天頂方向(根據觀測者緯度的不同而變化)。
- :黑圈代表觀測者所在地周圍的地平線,它垂直於天頂向量,定義了觀測者可見的天球部分。
- :紅點表示天頂和天底(天球上相對於觀測者與天頂相對的點)。
- :橙色圓圈代表天球子午線(或對觀測者來說,從地平線的正北方經過天頂至地平線正南方的子午線)。
- :紅圈代表一條相對於觀測者地平經線,在東方40°的次子午線。與所有次子午線一樣,它在天頂和天底與主子午線相交。
- :天球的地理南面是投影極。
- :赤道平面用作投影平面。
投影天球子午線時,會產生一條與天頂和天底所在的鼓室垂直軸重疊的直線。然而,當投影東方40°的次子午線時,會獲得另一個同時穿過天頂和天底投影的圓,因此其中心位於連接兩個點的線段的垂直平分線上。實際上,天球子午線的投影可以被認為是一個半徑無限大的圓(一條直線),其中心位於該平分線上,距離這兩點無窮遠。
如果投影將天球劃分為相等扇區的連續子午線(如從天頂輻射的「橙色切片」),則可以獲得穿過天頂投影在鼓室上的曲線族。這些曲線一旦與包含主要恆星的「軌道」重疊,就可以確定位於「軌道」上旋轉時,在一天中特定時間的恆星方位。
相關條目
- 水手星盤
- 中古伊斯蘭天文學
- 天文儀器列表
- 菲利普·丹弗里:數學儀器、地球儀和星盤的設計和製造商。
- 六分儀
- 渾儀
- 行星定位儀
- Yantraraja
參考資料
- 腳註
- Modern editions of John Philoponus' treatise on the astrolabe are De usu astrolabii eiusque constructione libellus (On the Use and Construction of the Astrolabe), ed. Heinrich Hase, Bonn: E. Weber, 1839, OCLC 165707441 (or id. Rheinisches Museum für Philologie 6 (1839): 127–71); repr. and translated into French by Alain Philippe Segonds, Jean Philopon, traité de l'astrolabe, Paris: Librairie Alain Brieux, 1981, OCLC 10467740; and translated into English by H.W. Green in R.T. Gunther, The Astrolabes of the World, Vol. 1/2, Oxford, 1932, repr. London: Holland Press, 1976, pp. 61–81.
- O'Leary, De Lacy. . Routledge and Kegan Paul. 1948 [2022-07-22]. (原始内容存档于2020-11-12).。"這一時期的後期最傑出的敘利亞學者是肯尼斯林主教西弗勒斯·塞博赫特(卒於666-7年)。[...]除了這些作品[...],他還撰寫了關於天文學主題的論文(Brit. Mus. Add. 14538),並撰寫了一篇關於星盤的天文儀器的論文,該論文由F. Nau(巴黎,1899年)編輯和出版。"
Severus' treatise was translated by Jessie Payne Smith Margoliouth in R.T. Gunther, Astrolabes of the World, Oxford, 1932, pp. 82–103. - Savage-Smith, Emilie. . Journal of Islamic Studies. 1993, 4 (2): 296–299. doi:10.1093/jis/4.2.296.
沒有證據表明球面星盤起源於希臘,但迄今為止已有的證據表明,它可能是一個早期但明顯的在伊斯蘭發展,沒有希臘的先例。
- 註解
- Northrup, Cynthia Clark; Bentley, Jerry H.; Eckes Jr., Alfred E. . Taylor and Francis, 2015. 2015: 72. ISBN 9781317471530.
- Morrison, Robert G. . Lindberg, David C.; Shank, Michael H. (编). . 2, Medieval Science. Cambridge: Cambridge University Press. 2013: 115 [15 May 2018]. ISBN 978-0-521-59448-6.
- Greenwood, William. . YouTube. January 28, 2018. (原始内容存档于2021-11-07).
- . Oxford English Dictionary 2nd. 1989.
- . Oxford Dictionaries. [2022-07-22]. (原始内容存档于2016-06-08).
- . Etymonline.com. [2013-11-07]. (原始内容存档于2017-08-08).
- King 1981,第44頁.
- King 1981,第51頁.
- King 1981,第45頁.
- Lewis 2001.
- Michael Deakin (August 3, 1997). "Ockham's Razor: Hypatia of Alexandria". ABC Radio. Retrieved July 10, 2014.
- Theodore, Jonathan. . Manchester, England: Palgrave, Macmillan. 2016: 183. ISBN 978-1-137-56997-4.
- Deakin, Michael A. B. . Amherst, New York: Prometheus Books. 2007: 102–104. ISBN 978-1-59102-520-7.
- Bradley, Michael John. . New York City, New York: Infobase Publishing. 2006: 63. ISBN 9780816054237.
- Sebokht, Severus. . Tertullian.org. [2022-07-22]. (原始内容存档于2018-10-21).
- See p. 289 of Martin, L. C., , Transactions of the Optical Society, 1923, 24 (5): 289–303, Bibcode:1923TrOS...24..289M, ISSN 1475-4878, doi:10.1088/1475-4878/24/5/302.
- Berggren, J. Lennart, , Katz, Victor J. (编), , Princeton University Press: 519, 2007, ISBN 978-0-691-11485-9
- Richard Nelson Frye: Golden Age of Persia. p. 163
- Dr. Emily Winterburn (National Maritime Museum), Using an Astrolabe (页面存档备份,存于), Foundation for Science Technology and Civilisation, 2005.
- Lachièz-Rey, Marc; Luminet, Jean-Pierre. . Trans. Joe Laredo. Cambridge, UK: Cambridge University Press. 2001: 74. ISBN 978-0-521-80040-2.
- 約翰·J·奧康納; 埃德蒙·F·羅伯遜, , (英语)
- Bedini, Silvio A.; Maddison, Francis R. . Transactions of the American Philosophical Society. 1966, 56 (5): 1–69. JSTOR 1006002. doi:10.2307/1006002.
- . Qantara-med.org. [2013-11-07]. (原始内容存档于2016-03-03).
- Nancy Marie Brown (2010), "The Abacus and the Cross". Page 140. Basic Books. ISBN 978-0-465-00950-3
- Boyle, David. . Bloomsbury Publishing USA. 2011: 253. ISBN 9780802779786..
- Northrup, Cynthia Clark (编). Enhanced Credo. Armonk, New York: Routledge. 2015: 72. ISBN 978-0765680587. OCLC 889717964.
- . The Astrolabe: an Online Resource. 2006 [2020-05-15]. (原始内容存档于2022-06-22).
- Harley, J. B.; Woodward, David. . Chicago: Univ. of Chicago Press. 1992: 31. ISBN 0-226-31635-1.
- Kunitzsch, Paul. . Archives Internationales d'Histoire des Sciences Oxford. 1981, 31 (106): 42–62.
- Selin, Helaine.
 . Springer Science & Business Media. 2008-03-12: 1335. ISBN 978-1-4020-4559-2.
. Springer Science & Business Media. 2008-03-12: 1335. ISBN 978-1-4020-4559-2. Paul Kunitzsch has recently established that the Latin treatise on the astrolabe long ascribed to Ma'sh'allah and translated by John of Seville is in fact by Ibn al-Saffar, a disciple of Maslama al-Majriti.
- Glick, Thomas; et al (编), , Routledge: 464, 2005, ISBN 0-415-96930-1
- Northrup, Cynthia Clark (编). [Enhanced Credo edition]. Armonk, New York: Routledge. 2015: 460. ISBN 978-0765680587. OCLC 889717964.
- Nancy Marie Brown (2010), "The Abacus and the Cross". Page 143. basic Books. ISBN 978-0-465-00950-3
- Hockey, Thomas. . Springer Publishing. 2009 [August 22, 2012]. ISBN 978-0-387-31022-0. (原始内容存档于2014-10-12).
- Ralf Kern (2010), Wissenschaftliche Instrumente in ihrer Zeit. Band 1: Vom Astrolab zum mathematischen Besteck. Cologne, S. 204. ISBN 978-3-86560-865-9
- North 2005.
- . Ulysse Nardin. (原始内容存档于2 January 2011).
- . [2022-08-01]. (原始内容存档于2012-06-20).
- Stephenson, Bruce; Bolt, Marvin; Friedman, Anna Felicity. . Cambridge, UK: Cambridge University Press. 2000: 108–109. ISBN 0-521-79143-X.
- . Ian Ridpath. [2016-11-12]. (原始内容存档于2018-10-17).
- King, David A. . Florence. : 30.
- King, David A. . Frankfurt: Frankfurt. 2018.
- Mayer, L.A. . A. Kunding. 1956. Bibcode:1956iatw.book.....M.
- Gentili, Graziano; Simonutti, Luisa; Struppa, Daniele C. . Journal of Humanistic Mathematics. 2020, 10: 101–144 [2023-12-31]. S2CID 211008813. doi:10.5642/jhummath.202001.07
 . (原始内容存档于2023-12-06).
. (原始内容存档于2023-12-06).
- 書目
- Evans, James, , Oxford University Press, 1998, ISBN 0-19-509539-1.
- Gunella, Alessandro; Lamprey, John, , John Lamprey, 2007
- King, D. A, , Journal for the History of Arabic Science, 1981, 5: 43–83
- King, Henry, , University of Toronto Press, 1978
- Krebs, Robert E.; Krebs, Carolyn A., , Greenwood Press, 2003.
- Laird, Edgar, Carol Poster and Richard Utz , 编, , Constructions of Time in the Late Middle Ages (Evanston, Illinois: Northwestern University Press), 1997: 51–69
- Laird, Edgar; Fischer, Robert (编), , Medieval & Renaissance Texts & Studies (Binghamton, New York), 1995, ISBN 0-86698-132-2
- Lewis, M. J. T., , Cambridge University Press, 2001.
- Morrison, James E, , Janus, 2007, ISBN 978-0-939320-30-1.
- Neugebauer, Otto E, , Springer, 1975
- North, John David, , Continuum International Publishing Group, 2005, ISBN 978-1-85285-451-5
外部連結
- Interactive digital astrolabe by Alex Boxer (页面存档备份,存于)
- A digital astrolabe (HTML5 and javascript) (页面存档备份,存于)
- Astrolabe Tech Made ... Not So Easy (页面存档备份,存于)
- paper astrolabe generator, from the ESO (页面存档备份,存于)
- "Hello World!" for the Astrolabe: The First Computer (页面存档备份,存于) Video of Howard Covitz's Presentation at Ignite Phoenix, June 2009. Slides for Presentation (页面存档备份,存于) Licensed as Creative Commons by-nc-nd.
- Video of Tom Wujec demonstrating an astrolabe. (页面存档备份,存于) Taken at TEDGlobal 2009. Includes clickable transcript. Licensed as Creative Commons by-nc-nd.
- Archive of James E. Morrison's extensive website on Astrolabes
- A working model of the Dr. Ludwig Oechslin's Astrolabium Galileo Galilei watch (页面存档备份,存于)
- Ulysse Nardin Astrolabium Galilei Galileo: A Detailed Explanation (页面存档备份,存于)
- Fully illustrated online catalogue of world's largest collection of astrolabes (页面存档备份,存于)
- Mobile astrolabe and horologium (页面存档备份,存于)
- Medieval equal hour horary quadrant (页面存档备份,存于)
- (PDF), [2018-10-26], (原始内容 (PDF)存档于2015-06-17)







.jpg.webp)