最大公因數
最大公因數(英語:,)也稱最大公約數(英語:,)是數學詞彙,指能够整除多個非零整數的最大正整数。例如8和12的最大公因数为4。
整数序列的最大公因数可以記為或。
最大公因数的值至少為1,例如;最大則為該組整數中絕對值最小的絕對值,例如和。
求兩個整數最大公因數主要的方法:
兩個整數的最大公因數和最小公倍數()的關係為:
兩個整數的最大公因數可用於計算兩數的最小公倍數,或分數化簡成最簡分數。
兩個整數的最大公因數和最小公倍數中存在分配律:
在直角坐標中,兩頂點為的線段會通過個格子點。
概述
例子
54和24的最大公因数是多少?
数字54可以表示為几组不同正整數的乘積:
故54的正因數為。
同樣地,24可以表示為:
故24的正因數為。
这两组数列中的共同元素即为54和24的公因数:
其中的最大數6即為54和24的最大公因數,記為:
互质数
如果两数的最大公因数为1,那么这两个数互質。例如,9和28就是互质数。
几何角度的说明

假设有一个大小为24乘60的矩形区域,这个区域可以按照不同的大小划分正方形网格:1乘1、2乘2、3乘3、4乘4、6乘6、12乘12。因此,12是24和60的最大公因数。大小为24乘60的矩形区域,可以按照12乘12的大小划分正方形网格,一边有两格()、另一边有五格()。
计算
质因数分解法
可以通过質因數分解来计算最大公因数。例如计算,可以先进行质因数分解 和 ,因为其中表达式的「重合」,所以。实践中,这种方法只在数字比较小时才可行,因为对较大数进行质因数分解通常会耗费大量的时间。
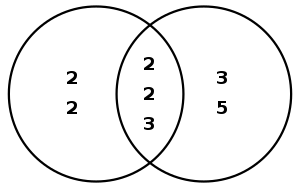
再举一个用文氏图表示的例子,计算48和180的最大公因数。首先对这两个数进行质因数分解:
它们之中的共同元素是两个2和一个3:
- 最小公倍数
- 最大公因数
辗转相除法
相比质因数分解法,辗转相除法的效率更高。
计算时,先将48除以18得到商2、余数12,然后再将18除以12得到商1、余数6,再将12除以6得到商2、余数0,即得到最大公因数6。我们只关心每次除法的余数是否为0,为0即表示得到答案。这一算法更正式的描述是这样的:
其中
如果参数都大于0,那么该算法可以写成更简单的形式:
- ,
- 如果 a > b
- 如果 b > a
程式代碼
以下使用輾轉相除法實現。
C#
private int GCD(int a, int b) {
if(0 != b) while(0 != (a %= b) && 0 != (b %= a));
return a + b;
}
C++
运行时计算实现:
template<typename T>
T GCD(T a, T b) {
if(b) while((a %= b) && (b %= a));
return a + b;
}
编译时计算实现:
#include <iostream>
#include <type_traits>
template<typename T, std::enable_if_t<std::is_integral<T>::value, T> a, std::enable_if_t<std::is_integral<T>::value, T> b>
struct HCF{
public:
static const T value=HCF<T, (a>b? b: a), (a>b? a%b: b%a)>::value;
};
template<typename T, std::enable_if_t<std::is_integral<T>::value, T> a>
struct HCF<T, a, 0>{
public:
static const T value=a;
};
int main(){
std::wcout<<HCF<int, 12, 64>::value<<std::endl;//Output: 4
}
C
int GCD(int a, int b) {
if (b) while((a %= b) && (b %= a));
return a + b;
}
Java
private int GCD(int a, int b) {
if (b==0) return a;
return GCD(b, a % b);
}
JavaScript
const GCD = (a, b) => b ? GCD(b, a % b) : a;
Python
GCD = lambda a, b: (a if b == 0 else GCD(b, a % b))
# or
def GCD(a, b):
if b == 0:
return a
return GCD(b, a % b)
政治用法
最大公約數又指一社會中不同陣營勉強所達之共同利益。
参考文献
- . [2018-06-11]. (原始内容存档于2020-09-22).
参见
- 公倍数
- 公约数
- 最小公倍数