算術邏輯單元
算术逻辑单元(英語:,縮寫:ALU)是一种可对二进制整数执行算术运算或位运算的组合逻辑数字电路。[1][2][3][4]ALU 与浮点数运算单元(FPU)不同,后者仅对浮点数进行操作。ALU 是许多类型的计算电路的基本部件,这些计算电路包括计算机的中央处理单元(CPU)、浮点处理单元(FPU)和图形处理单元(GPU)。单个CPU、FPU 或 GPU 可能包含多个 ALU。
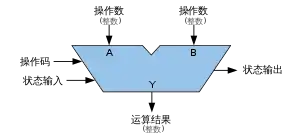
ALU 的输入包括需要运算的数据(也称为运算数)和表明了运算操作类型的指令码。ALU 的输出是其执行运算的结果。在许多的设计中,ALU 还带有状态输入或输出,可将其之前操作或当前操作的信息在 ALU 和外部状态寄存器间传递。
信号
一个 ALU 具有各种输入和输出网络,它们用于在 ALU 和外部电路之间传送数字信号。当 ALU 工作时,外部电路在 ALU 的输入端输入信号,而 ALU 将产生运算结果,并将信号通过其输出端输出至外部电路。
数据
一个基本的 ALU 具有三个并行的数据总线,包括两个输入操作数(A、B)和结果输出(Y)。每个数据总线都是一组传递了一个二进制整数的信号。通常,A、B和Y的总线宽度(每个总线包含的信号数)是相同的,并且与外部电路(例如,封装 CPU 或其他处理器)的原生字长相同。
操作码
操作码通过并行总线输入,它向 ALU 传递选择的操作的信息,该操作选择码是对 ALU 要执行的算术或逻辑运算的枚举。操作码的长度(其总线宽度)决定了 ALU 可以执行的操作的最大数量。例如,一个4位操作码可最多为 ALU 指定不同的 16 个操作(16=24)。通常,ALU 的操作码与机器语言的操作码不同,尽管在某些情况下,它可以直接编码为机器语言操作码内的位字段。
输出
ALU 的状态输出是各类单独的信号,补充表示了有关当前 ALU 操作结果的信息。通用 ALU 通常具有以下状态信号:
- Carry-out,表示由加法运算产生的进位、由减法运算产生的借位或由二进制移位运算产生的溢出位。
- Zero,表示运算结果的所有位均为逻辑零。
- Negative,表示算术运算结果为负。
- Overflow,表示算术运算的结果溢出,超出了 Y 的数值范围。
- Parity,表示输出数 Y 的奇偶校验结果,说明 Y 中的含有逻辑 1 的数量的奇偶性。
在 ALU 的操作结束后,状态输出信号通常会被存储在外部寄存器中,以使其可用于之后的 ALU 操作(例如实现多倍精度运算,或用于控制条件分支)。存储了状态输出的集合的位寄存器通常被视为一整个多位寄存器,称为“状态寄存器”或“条件代码寄存器”。
输入
状态输入使 ALU 在执行操作时可接收其他信息。通常,这是单个“低位进位”,传递了来自上一级 ALU 操作的进位。
电路操作
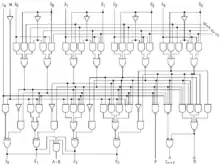
ALU 是组合逻辑电路。这意味着当输入变化时,其输出也将随之变化。在正常的情况下输入到 ALU 的信号是稳定的,并且当经过足够的时间(称为“传播延迟”)信号通过 ALU 中的电路传播后,ALU 操作的结果就会出现在ALU上输出。连接到 ALU 的外部电路负责确保 ALU 的输入信号在整个操作过程中是稳定的,并在对 ALU 的输出进行采样之前为信号传播预留足够的时间。
通常,外部电路通过将信号施加到其输入端来控制 ALU。外部电路往往采用顺序逻辑来控制 ALU 的运作,该操作由足够低频率的时钟信号调整,以确保 ALU 的输出在最坏情况下也有足够的时间达到稳定。
例如,在用 ALU 执行加法操作时,CPU 会将操作数(通常是从寄存器)路由到 ALU 的输入,而控制单元会同时将一个值传送至 ALU 的操作码输入,使其执行加法操作。同时,CPU 还将把 ALU 的计算结果输出路由到用于接收该结果的目标寄存器。在 CPU 等待下一个时钟期间,ALU 的输入信号需一直保持稳定,已使其通过 ALU 并到达目标寄存器。当下一个时钟到达时,目标寄存器将存储 ALU 结果,并且由于 ALU 操作已完成,因此此时可以为下一次 ALU 操作设置 ALU 输入。
功能
ALU 通常支持许多基本算术和按位逻辑函数。基本的通用 ALU 通常支持以下操作[1][2][3][4]:
算术运算
- 加法:将操作数 A、B 相加,并在 Y 处得到二者的和
- 带进位加法:将操作数 A、B、进位相加,并在 Y 处得到三者的和
- 减法:将操作数 A、B 相减,并在 Y 处得到二者的差。对于此功能,结转实际上是“借入”指示器。此操作也可以用来比较A和B的大小;在这种情况下,处理器可能会忽略Y输出,该处理器仅对操作产生的状态位(尤其是零和负)感兴趣。
- 带借位减法:借位(进位)从A中减去B(反之亦然),差值出现在Y处并结转(借入)。
- 二补数(取相反数):得到 A 或 B 的相反数(将 0 与 A 相减或将 0 与 B 相减),并在 Y 处得到计算结果
- 加 1:将 A(或 B)增加 1,并在 Y 处得到计算结果
- 减 1:将 A(或 B)减小 1,并在 Y 处得到计算结果
- 直通(Pass through):保持 A(或 B)的所有位不变,并在 Y 处得到原输入数;该操作常用于对操作数进行奇偶校验,判断是否为 0,判断是否为负数,或者为了将操作数直接加载到寄存器中。
按位逻辑运算
- AND:将 A 和 B 按位进行“与”运算,并在 Y 处得到计算结果
- OR:将 A 和 B 按位进行“或”运算,并在 Y 处得到计算结果
- XOR:将 A 和 B 按位进行“异或”运算,并在 Y 处得到计算结果
- 补码:将 A(或 B)的每一位都反转,并在 Y 处得到计算结果
移位操作
| 类型 | 左移 | 右移 |
|---|---|---|
| 算术移位 |  |
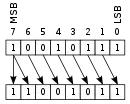 |
| 逻辑移位 |  |
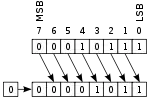 |
| 循环移位 | 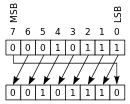 |
 |
| 循环移位
(带进位) |
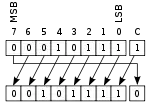 |
 |
在不同的操作码下,ALU 的移位操作可将操作数 A(或 B)向左或向右移位,移位的结果将出现在 Y 处。简单的 ALU 通常只能将操作数移位一位,而更复杂的 ALU 使用桶形移位器,在一次操作中可移位任意的位数。在一位的移位操作中,从操作数移出的位会被转移到进位输出中。而被移位到操作数中的数位取决于移位的类型,比如:
- 算术移位:操作数被视为二补数整数,其高有效位是符号位,在移位时会被保留。
- 逻辑移位:移位时用逻辑 0 补充操作数,这适合于无符号整数。
- 循环移位:此时操作数被视为一个循环缓冲区,因此在移位时,其最低和最高位就像是相邻的。
- 循环移位(带进位):进位输入(C)和操作数被视为整个操作数的循环移位。
应用
多倍精度运算
在整数算术计算中,多倍精度运算(Multiple-precision arithmetic)是对字长大于 ALU 字长的整数进行运算的操作。为此,该算法将每个操作数视为多个 ALU 能够处理的操作数片段的集合(并从最高位(MSB)到最低位(LSB)排列,或相反)。例如,在使用 8 位 ALU 的情况下,将 24 位整数0x123456视为如下三个8位片段的集合:0x12(高位)、0x34、0x56(低位)。由于片段的大小与该 ALU 字长完全匹配,因此可以直接对这几个数进行操作。
该算法使用 ALU 直接对特定的操作数片段进行运算,从而生成多精度结果的相应片段。在操作数的每个片段被计算后,结果都将被保存到对应的位置。对所有操作数片段重复此过程,将这些结果进行拼合,即可得到完整的运算结果。
对于算术运算(如加法和减法),该算法首先对操作数的最低位片段进行运算,从而生成最低位对应的结果和进位。随后将该结果储存至某个指定的位置,而处理器通常会存储 ALU 状态输出中的进位。然后,该算法继续计算每个操作数片段集合的下一个片段,并对这些片段调用 ALU 操作,并将先前 ALU 操作的进位一起输入,从而产生另一个更高位的片段和进位。重复此过程,直到处理完所有操作数片段为止,从而在存储位置中得到完整的运算结果。
对于移位运算,操作数片段处理的顺序取决于移位方向。在左移操作中,首先对最低位片段进行处理,因为必须用低位片段左移的溢出位来得到该运算的最低位。类似地,在右移操作中应首先对操作数的最高位进行处理。
对于按位逻辑运算(如逻辑与、逻辑或操作)中,可以按任何任意顺序处理操作数片段,因为计算结果的每个片段仅取决于相应的操作数片段(来自先前 ALU 操作的进位将被忽略)。
复杂运算
尽管可以将ALU设计于执行复杂的功能,但在许多情况下,由此导致的更高的电路复杂性,成本,功耗和更大的尺寸使其不切实际。因此,ALU通常限于可以以非常高的速度(传播延迟更短)执行的简单功能,而为了执行复杂的运算,外部处理器电路则需要将一系列简单的ALU操作进行编排。
例如,在ALU的复杂程度不同的情况下,可以通过多种方式来计算数字的平方根:
- 单周期计算:如果一个ALU设计得足够复杂,那它可能可在一次操作中得到计算结果。
- 计算流水线:可以让一组结构不那么复杂的 ALU 逐步地完成平方根计算,计算的中间结果储存在各级 ALU 上,就像工厂的生产线一样。该电路可以在完成之前的操作数前接受新的操作数,并得到与复杂的 ALU 一样快的结果,尽管结果过程会因各级 ALU 的延迟而存在延迟。有关更多信息,请参见指令流水线。
- 迭代计算:可让 ALU 在控制单元的控制下经由多步计算平方根,这使其结构更加简单。
上面的实现从最快和最昂贵的到最慢和最便宜的过渡,在这几种情况下都可完成平方根的计算,但是结构更加简单的 ALU 的计算时间往往更长,因为需要执行多步操作。
实现
ALU 通常是一个独立的集成电路(如 74181 芯片),也可能是一个更加复杂的 IC 的一部分。在后一种情况下,ALU 一般由VHDL、Verilog或其他硬件描述语言编写,并通过综合该代码来实例化其电路。例如,以下 VHDL 代码描述了一个功能非常简单的8位ALU:
entity alu is
port ( -- 该 ALU 对外部电路的接口
A : in signed(7 downto 0); -- 操作数 A
B : in signed(7 downto 0); -- 操作数 B
OP : in unsigned(2 downto 0); -- 运算指令
Y : out signed(7 downto 0)); -- 运算结果
end alu;
architecture behavioral of alu is
begin
case OP is -- 解码运算指令并执行计算操作
when "000" => Y <= A + B; -- 加法
when "001" => Y <= A - B; -- 减法
when "010" => Y <= A - 1; -- 减1
when "011" => Y <= A + 1; -- 加1
when "100" => Y <= not A; -- 求补
when "101" => Y <= A and B; -- 位与
when "110" => Y <= A or B; -- 位或
when "111" => Y <= A xor B; -- 位异或
when others => Y <= (others => 'X');
end case;
end behavioral;
历史
冯·诺伊曼在1945年的一份关于新型计算机EDVAC的基础的报告中提出了 ALU 的概念。[5]
在整个信息时代的初期,电子电路的成本,尺寸和功耗都相对较高。因此,尽管所有串行计算机和许多早期计算机(例如 PDP-8)都具有一个简单的 ALU,但它一次只能处理一个数据位,而程序员们使用更长的字长。最早的具有多个分立单位 ALU 电路的计算机是1948年的 Whirlwind I,它使用了16个这样的“数学单元”,以使其能够对16位数据进行操作。
1967年,仙童半导体推出了第一款用集成电路实现的 ALU,名为 Fairchild 3800,由一个带累加器的八位 ALU 构成[6]。随后,其他集成电路 ALU 也相继出现,包括4位 ALU,如 Am2901 和 74181。这些设备通常具有“位片”功能,这意味着它们可以输出“超前进位”的信号,从而有助于使用多个 ALU 芯片相互连接以构成字长更宽的 ALU。这些设备迅速流行起来,并广泛用于位片微型计算机。
1970年代初,微处理器开始出现。虽然晶体管变得越来越小,但裸晶的尺寸并不足以放下全字宽的 ALU。因此,一些早期的微处理器采用了位数更少的 ALU,每条指令因而需要多个周期来执行。比如当时流行的Zilog Z80,它使用4位 ALU 执行8位加法运算。[7]后来,正如摩尔定律预测的那样,晶体管的尺寸进一步缩小,在微处理器上构建更宽的 ALU 从而也变得可行。
现代的集成电路中晶体管的尺寸比早期微处理器的小几个数量级,从而可以配备高度复杂的 ALU。如今,许多现代ALU的字宽更宽,体系结构的提升(如使用了桶形移位器和二进制乘法器)能使它们能够在单个时钟周期内执行需要早期 ALU 进行多次运算才能完成的操作。
参见
- 加法器
- 乘法器
- 地址生成单元
- 加载存储单元
- 执行单元
参考资料
- A.P.Godse; D.A.Godse. . Technical Publications. 2009: 9–3. ISBN 978-81-8431-738-1.
- . Headquarters, Department of the Army. 2001: 371–.
- A.P.Godse; D.A.Godse. . Technical Publications. 2009: C–1. ISBN 978-81-8431-650-6.
- Horowitz, Paul; Winfield Hill. 2nd. Cambridge University Press. 1989: 990–. ISBN 978-0-521-37095-0.
- Philip Levis. (PDF). cs.berkeley.edu: 1, 3. November 8, 2004 [January 20, 2015]. (原始内容 (PDF)存档于September 23, 2015).
- Lee Boysel. . U. Mich. EECS Presentation / ECE Recordings. 2007-10-12. (原始内容存档于2012-11-15).
- Ken Shirriff. "The Z-80 has a 4-bit ALU. Here's how it works." (页面存档备份,存于) 2013, righto.com
延伸阅读
- Hwang, Enoch. . Thomson. 2006 [2020-08-30]. ISBN 0-534-46593-5. (原始内容存档于2008-10-12).
- Stallings, William. 7th. Pearson Prentice Hall. 2006 [2020-08-30]. ISBN 0-13-185644-8. (原始内容存档于2007-10-24).