過適
在統計學中,過適(英語:,或稱擬合過度)是指過於緊密或精確地匹配特定資料集,以致於無法良好地拟合其他資料或預測未來的觀察結果的現象。[1]过拟合模型指的是相较有限的数据而言,参数过多或者结构过于复杂的统计模型。[2]发生过拟合时,模型的偏差小而方差大。过拟合的本质是训练算法从统计噪声中不自觉获取了信息并表达在了模型结构的参数当中。[3]:45相较用于训练的資料總量來說,一個模型只要结构足夠複雜或参数足够多,就总是可以完美地適應資料的。過適一般可以視為違反奥卡姆剃刀原則。

与过拟合相对应的概念是欠拟合(英語:,或稱:擬合不足);它是指相较于数据而言,模型参数过少或者模型结构过于简单,以至于无法捕捉到数据中的规律的现象。发生欠拟合时,模型的偏差大而方差小。
在机器学习或人工神經網路中,过拟合与欠拟合有时也被称为「过训练(英語:)」和「欠训练(英語:)」。
之所以存在过拟合的可能,是因为选择模型的标准和评价模型的标准是不一致的。举例来说,选择模型时往往是选取在训练数据上表现最好的模型;但评价模型时则是观察模型在训练过程中不可见数据上的表现。当模型尝试「记住」训练数据而非从训练数据中学习规律时,就可能发生过拟合。一般来说,當參數的自由度或模型结构的复杂度超過資料所包含資訊內容時,拟合后的模型可能使用任意多的參數,這會降低或破壞模型泛化的能力。
在統計学习和機器學習中,為了避免或减轻過適現象,須要使用額外的技巧(如模型选择、交叉驗證、提前停止、正则化、剪枝、贝叶斯信息量准则、赤池信息量準則或dropout)。在treatment learning中,使用最小最佳支援值(英語:)來避免過適。这些方法大致可分为两类:1. 对模型的复杂度进行惩罚,从而避免产生过于复杂的模型;2. 在验证数据上测试模型的效果,从而模拟模型在实际工作环境的数据上的表现。
机器学习
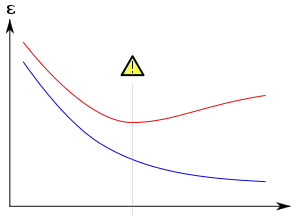
机器学习模型的典型产出过程是由机器学习算法在训练集上进行训练,希望得到的模型能够在训练过程中不可见的验证集上表现良好。过拟合现象发生在使用违反奥卡姆剃刀原则的模型或算法时:当引入相较数据集而言过多的参数时,或使用相较数据集而言过于复杂的模型时。
假设有一个训练集,其基准真相 y 可以用一个二元线性函数很好地预测出来。显而易见,该函数只有3个参数:一个截距,两个斜率。将该函数替换成更为复杂的二次函数或更多元的线性函数的风险在于:奥卡姆剃刀表明,相较于给定的简单函数,任何给定的复杂函数的预测都更不可靠。[4]:358如果最终选择了复杂函数而非简单函数;并且在拟合训练数据时相较简单函数,复杂函数带来的收益没有抵消模型复杂度的增加,那么复杂函数就过拟合了数据。此时,尽管复杂函数在训练集上的表现与简单函数相同甚至更好,但在训练数据之外的验证数据上的表现,复杂函数可能会更糟糕。[5]
在确定模型复杂度时,简单地计算各模型中参数的数量是不可靠的,还需要考虑参数的表达方式。举例来说,直接比较带有 m 个参数的神经网络(它能够跟踪非线性关系)和带有 n 个参数的回归模型是非平凡的。[5]
过拟合尤其容易在训练迭代次数相对有限训练样本过多的时候。此时,模型会拟合训练数据中特征的随机噪声,而这些与目标函数之间并无因果关系。在这种过拟合的过程中,模型在训练样本上的效果会持续提升,但在训练中不可见的数据(通常是验证集)上的效果会变得更差。举个简单的例子:假设有一个数据集,其中包含了零售的物品、买家、购买日期、购买时间。人们很容易在这个数据集上构造模型,来根据购买日期和购买时间预测其他属性;但该模型在新数据上没有任何泛化性能,因为过去的时间再也不会出现了。
概括地说,机器学习算法在已知数据上很精确但在新数据上不精确的情形,可以称之为过拟合。人们可以这样在直觉上理解过拟合:「过去的经验可被分为两个部分:与将来有关的数据、与将来无关的数据(噪声)」。在其他条件都相同的情况下,预测的难度越大(不确定性越高),则过去信息中需要被当做噪声忽略的部分就越多。问题的难点在于,如何确定哪些数据应当被忽略。
能够避免拟合噪声的机器学习算法是健壮的算法。
后果
过拟合最显著的后果就是在验证集上的效果很差;其他后果罗列如下:[5]
- 相较拟合恰当的模型而言,拟合过度的模型倾向于从验证集的每个样本中获取更多信息;收集这些不必要的信息可能代价是高昂的,或者具有错误倾向的。当这些信息需要人工观察或者标注时,这种代价尤其明显。
- 拟合过度的复杂模型相较简单模型的可移植性更差。极端地说,一元线性回归模型可移植性非常好,甚至,但凡必要时,甚至可以用徒手进行计算。另一方面,极端复杂的模型只能在原始数据集上复现,这给模型的重用和理论研究的复现带来了困难。
扩展阅读
- 偏差-方差权衡
- 曲线拟合
- 数据清洗
- 特征选择
- Freedman悖论
- 泛化误差
- 拟合程度
- Life-time of correlation
- 模型选择
- 奥卡姆剃刀
- VC dimension
參考文獻
- OxfordDictionaries.com中overfitting (页面存档备份,存于)的統計學定義。
- Everitt B.S., Skrondal A. (2010), Cambridge Dictionary of Statistics, Cambridge University Press.
- Burnham, K. P.; Anderson, D. R., 2nd, Springer-Verlag, 2002. (This has over 44000 citations on Google Scholar.)
- Francesco Pezzella, Mahvash Tavassoli, David Kerr. . Oxford University Press.
- Hawkins, Douglas M. (2004), "The problem of overfitting", Journal of Chemical Information and Modeling, 44.1: 1–12.
外部連結
- http://www.cs.sunysb.edu/~skiena/jaialai/excerpts/node16.html (页面存档备份,存于)
- 過度訓練 (页面存档备份,存于)(英文)
- 偏差方差权衡与过拟合 (页面存档备份,存于) (中文)