隐马尔可夫模型
隐马尔可夫模型(英語:;縮寫:),或稱作,是统计模型,用来描述一个含有隐含未知参数的马尔可夫过程。其难点是从可观察的参数中确定该过程的隐含参数。然后利用这些参数来作进一步的分析,例如模式识别。
| 机器学习与 |
|---|
 |
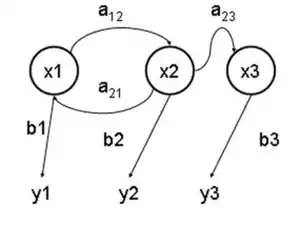
x — 隐含状态
y — 可观察的输出
a — 转换概率(transition probabilities)
b — 输出概率(output probabilities)
在正常的马尔可夫模型中,状态对于观察者来说是直接可见的。这样状态的转换概率便是全部的参数。而在隐马尔可夫模型中,状态并不是直接可见的,但受状态影响的某些变量则是可见的。每一个状态在可能输出的符号上都有一概率分布。因此输出符号的序列能够透露出状态序列的一些信息。
隐马尔可夫模型在热力学、统计力学、物理学、化学、经济学、金融学、信号处理、信息论、模式识别(如语音识别、[1]手写识别、手势识别、[2]词性标记、乐谱跟随[3])、局部放电[4]及生物信息学等领域都有应用。[5][6]
定义
令、为离散时间随机过程, 。则是隐马尔可夫模型的条件是:
- 是马尔可夫过程,其行为不可直接观测(“隐”);
- ,且对每个博雷尔集。
令、为连续时间随机过程。则是隐马尔可夫模型的条件是:
- 是马尔可夫过程,其行为不可直接观测(“隐”);
- ,
- 、每个博雷尔集且每族博雷尔集
术语
过程状态(或)称作隐状态,(或)称作条件概率或输出概率。
马尔可夫模型的演化
下边的图示强调了HMM的状态变迁。有时,明确的表示出模型的演化也是有用的,我们用 x(t1) 与 x(t2) 来表达不同时刻 t1 和 t2 的状态。
圖中箭頭方向則表示不同資訊間的關聯性,因此可以得知和有關,而又和有關。
而每個只和有關,其中我們稱為隱藏變數(hidden variable),是觀察者無法得知的變數。
隱性馬可夫模型常被用來解決有未知條件的數學問題。
假設隱藏狀態的值對應到的空間有個元素,也就是說在時間時,隱藏狀態會有種可能。
同樣的,也會有種可能的值,所以從到間的關係會有種可能。
除了間的關係外,每組間也有對應的關係。
若觀察到的有種可能的值,則从到的输出模型复杂度為。如果是一个维的向量,则从到的输出模型复杂度為。
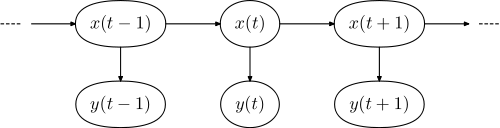
在这个图中,每一个时间块(x(t), y(t))都可以向前或向后延伸。通常,时间的起点被设置为t=0 或 t=1.
马尔可夫模型的機率
假設觀察到的結果為
隱藏條件為
長度為,則馬可夫模型的機率可以表達為:
由這個機率模型來看,可以得知馬可夫模型將該時間點前後的資訊都納入考量。
使用隐马尔可夫模型
HMM有三个典型(canonical)问题:
- 预测(filter):已知模型参数和某一特定输出序列,求最后时刻各个隐含状态的概率分布,即求 。通常使用前向算法解决。
- 平滑(smoothing):已知模型参数和某一特定输出序列,求中间时刻各个隐含状态的概率分布,即求 。通常使用前向-后向算法解决。
- 解码(most likely explanation):已知模型参数,寻找最可能的能产生某一特定输出序列的隐含状态的序列,即求 。通常使用Viterbi算法解决。
此外,已知输出序列,寻找最可能的状态转移以及输出概率.通常使用Baum-Welch算法以及Viterbi algorithm解决。另外,最近的一些方法使用联结树算法来解决这三个问题。
具体实例
假设你有一个住得很远的朋友,他每天跟你打电话告诉你他那天做了什么。你的朋友仅仅对三种活动感兴趣:公园散步,购物以及清理房间。他选择做什么事情只凭天气。你对于他所住的地方的天气情况并不了解,但是你知道总的趋势。在他告诉你每天所做的事情基础上,你想要猜测他所在地的天气情况。
你认为天气的运行就像一个马尔可夫链。其有两个状态「雨」和「晴」,但是你无法直接观察它们,也就是说,它们对于你是隐藏的。每天,你的朋友有一定的概率进行下列活动:「散步」、「购物」、「清理」。因为你朋友告诉你他的活动,所以这些活动就是你的观察数据。这整个系统就是一个隐马尔可夫模型(HMM)。
你知道这个地区的总的天气趋势,并且平时知道你朋友会做的事情。也就是说这个隐马尔可夫模型的参数是已知的。你可以用程序语言(Python)写下来:
states = ('Rainy', 'Sunny')
observations = ('walk', 'shop', 'clean')
start_probability = {'Rainy': 0.6, 'Sunny': 0.4}
transition_probability = {
'Rainy' : {'Rainy': 0.7, 'Sunny': 0.3},
'Sunny' : {'Rainy': 0.4, 'Sunny': 0.6},
}
emission_probability = {
'Rainy' : {'walk': 0.1, 'shop': 0.4, 'clean': 0.5},
'Sunny' : {'walk': 0.6, 'shop': 0.3, 'clean': 0.1},
}
在这些代码中,start_probability代表了你对于你朋友第一次给你打电话时的天气情况的不确定性(你知道的只是那个地方平均起来下雨多些)。在这里,这个特定的概率分布并非平衡的,平衡概率应该接近(在给定变迁概率的情况下){'Rainy': 0.571, 'Sunny': 0.429}。
transition_probability 表示基于马尔可夫链模型的天气变迁,在这个例子中,如果今天下雨,那么明天天晴的概率只有30%。代码emission_probability 表示了你朋友每天做某件事的概率。如果下雨,有50% 的概率他在清理房间;如果天晴,则有60%的概率他在外头散步。
这个例子在维特比算法页上有更多的解释。
结构架构
下图展示了实例化HMM的一般结构。椭圆形代表随机变量,可采用多个数值中的任意一种。随机变量是t时刻的隐状态(图示模型中);随机变量y(t)是t时刻的观测值();箭头表示条件依赖关系。

图中可清楚看出,给定隐变量在时间t的条件概率分布只取决于隐变量的值,之前的则没有影响,这就是所谓马尔可夫性质。观测变量同理,只取决于隐变量的值。
在本文所述标准HMM中,隐变量的状态空间是离散的,而观测值本身则可以离散(一般来自分类分布)也可以连续(一般来自正态分布)。HMM参数有两类:转移概率与输出概率,前者控制时刻的隐状态下,如何选择t时刻的隐状态。
隐状态空间一般假设包含N个可能值,以分类分布为模型。这意味着,对隐变量在t时刻可能所处的N种状态中的每种,都有到时刻可能的N种状态的转移概率,共有个转移概率。注意从任意给定状态转移的转移概率之和须为1。于是,转移概率构成了N阶方阵,称作马尔可夫矩阵。由于任何转移概率都可在已知其他概率的情形下确定,因此共有个转移参数。
此外,对N种可能状态中的每种,都有一组输出概率,在给定隐状态下控制着观测变量的分布。这组概率的大小取决于观测变量的性质,例如,若观测变量是离散的,有M种值、遵循分类分布,则有个独立参数,所有隐状态下共有个输出概率参数。若观测向量是M维向量,遵循任意多元正态分布,则将有M个参数控制均值,个参数控制协方差矩阵,共有个输出参数。(这时,除非M很小,否则限制观测向量各元素间协方差的性质可能更有用,例如假设各元素相互独立,或假设除固定多相邻元素外,其他元素相互独立。)
学习
HMM的参数学习任务是指在给定输出序列或一组序列的情形下,找到一组最佳的状态转换和转移概率。任务通常是根据一组输出序列,得到HMM参数的最大似然估计值。目前还没有精确解这问题的可行算法,可用鲍姆-韦尔奇算法或Baldi–Chauvin算法高效地推导出局部最大似然。鲍姆-韦尔奇算法是最大期望算法的特例。
若将HMM用于时间序列预测,则更复杂的贝叶斯推理方法(如马尔可夫链蒙特卡洛采样法,MCMC采样法)已被证明在准确性和稳定性上都优于寻找单一的最大似然模型。[7]由于MCMC带来了巨大的计算负担,在计算可扩展性也很重要时,也可采用贝叶斯推理的变分近似方法,如[8]。事实上,近似变分推理的计算效率可与期望最大化相比,而精确度仅略逊于精确的MCMC型贝叶斯推理。
隐马尔可夫模型的应用
- 语音识别、中文斷詞/分詞或光学字符识别
- 机器翻译
- 生物信息学 和 基因组学
- 基因组序列中蛋白质编码区域的预测
- 对于相互关联的DNA或蛋白质族的建模
- 从基本结构中预测第二结构元素
- 通信中的译码过程
- 地图匹配算法
- 还有更多...
隐马尔可夫模型在語音處理上的應用
因為馬可夫模型有下列特色:
- 時間點的隱藏條件和時間點的隱藏條件有關。因為人類語音擁有前後的關聯,可以從語義與發音兩點來看:
- 單字的發音擁有前後關聯:例如"They are"常常發音成"They're",或是"Did you"會因為"you"的發音受"did"的影響,常常發音成"did ju",而且語音辨識中用句子的發音來進行分析,因此需要考慮到每個音節的前後關係,才能夠有較高的準確率。
- 句子中的單字有前後關係:從英文文法來看,主詞後面常常接助動詞或是動詞,動詞後面接的會是受詞或介係詞。而或是從單一單字的使用方法來看,對應的動詞會有固定使用的介係詞或對應名詞。因此分析語音訊息時需要為了提升每個單字的準確率,也需要分析前後的單字。
- 馬可夫模型將輸入訊息視為一單位一單位,接著進行分析,與人類語音模型的特性相似。語音系統辨識的單位為一個單位時間內的聲音。利用梅爾倒頻譜等語音處理方法,轉換成一個發音單位,為離散型的資訊。而馬可夫模型使用的隱藏條件也是一個個被封包的,因此使用馬可夫模型來處理聲音訊號比較合適。
历史
隐马尔可夫模型最初是在20世纪60年代后半期Leonard E. Baum和其它一些作者在一系列的统计学论文中描述的。HMM最初的应用之一是开始于20世纪70年代中期的语音识别。[9]
在1980年代后半期,HMM开始应用到生物序列尤其是DNA的分析中。此后,在生物信息学领域HMM逐渐成为一项不可或缺的技术。[10]
参见
- 安德雷·马尔可夫
- 贝叶斯推断
- 估计理论
- 條件隨機域
- 排队理论
- 馬可夫決策過程
注解
- . [2023-10-27]. (原始内容存档于2022-09-30).
- Thad Starner, Alex Pentland. Real-Time American Sign Language Visual Recognition From Video Using Hidden Markov Models (页面存档备份,存于). Master's Thesis, MIT, Feb 1995, Program in Media Arts
- B. Pardo and W. Birmingham. Modeling Form for On-line Following of Musical Performances 的存檔,存档日期2012-02-06.. AAAI-05 Proc., July 2005.
- Satish L, Gururaj BI (April 2003). "Use of hidden Markov models for partial discharge pattern classification (页面存档备份,存于)". IEEE Transactions on Dielectrics and Electrical Insulation.
- Li, N; Stephens, M. . Genetics. December 2003, 165 (4): 2213–33. PMC 1462870
 . PMID 14704198. doi:10.1093/genetics/165.4.2213.
. PMID 14704198. doi:10.1093/genetics/165.4.2213. - Ernst, Jason; Kellis, Manolis. . Nature Methods. March 2012, 9 (3): 215–216. PMC 3577932
 . PMID 22373907. doi:10.1038/nmeth.1906.
. PMID 22373907. doi:10.1038/nmeth.1906. - Sipos, I. Róbert. Parallel stratified MCMC sampling of AR-HMMs for stochastic time series prediction. In: Proceedings, 4th Stochastic Modeling Techniques and Data Analysis International Conference with Demographics Workshop (SMTDA2016), pp. 295-306. Valletta, 2016. PDF
- Chatzis, Sotirios P.; Kosmopoulos, Dimitrios I. (PDF). Pattern Recognition. 2011, 44 (2): 295–306 [2018-03-11]. Bibcode:2011PatRe..44..295C. CiteSeerX 10.1.1.629.6275
 . doi:10.1016/j.patcog.2010.09.001. (原始内容 (PDF)存档于2011-04-01).
. doi:10.1016/j.patcog.2010.09.001. (原始内容 (PDF)存档于2011-04-01). - Rabiner, p. 258
- Durbin
参考书目
- Lawrence R. Rabiner, A Tutorial on Hidden Markov Models and Selected Applications in Speech Recognition. Proceedings of the IEEE, 77 (2), p. 257–286, February 1989.
- Richard Durbin, Sean R. Eddy, Anders Krogh, Graeme Mitchison. Biological Sequence Analysis: Probabilistic Models of Proteins and Nucleic Acids. Cambridge University Press, 1999. ISBN 0521629713.
- Kristie Seymore, Andrew McCallum, and Roni Rosenfeld. Learning Hidden Markov Model Structure for Information Extraction. AAAI 99 Workshop on Machine Learning for Information Extraction, 1999. (also at CiteSeer: (页面存档备份,存于))
- http://www.comp.leeds.ac.uk/roger/HiddenMarkovModels/html_dev/main.html (页面存档备份,存于)
- J. Li (页面存档备份,存于), A. Najmi, R. M. Gray, Image classification by a two dimensional hidden Markov model, IEEE Transactions on Signal Processing, 48(2):517-33, February 2000.
- 隐马尔可夫模型(课件), 徐从富,浙江大学人工智能研究所
外部链接
- Hidden Markov Model (HMM) Toolbox for Matlab (by Kevin Murphy)
- Hidden Markov Model Toolkit (HTK) (页面存档备份,存于) (a portable toolkit for building and manipulating hidden Markov models)
- Hidden Markov Models (页面存档备份,存于) (an exposition using basic mathematics)
- GHMM Library (页面存档备份,存于) (home page of the GHMM Library project)
- Jahmm Java Library (Java library and associated graphical application)
- A step-by-step tutorial on HMMs (页面存档备份,存于) (University of Leeds)
- Software for Markov Models and Processes (TreeAge Software)