电阻
在電磁學裡,電阻(英語:)是一個物體對於電流通過的阻礙能力,以方程式定義為:
;
假設一个物體具有均勻截面面積,則其電阻與電阻率、長度成正比,與截面面積成反比。
在國際單位制中,電阻的單位為歐姆(Ω,Ohm)。電阻的倒數為電導,單位為西門子(S)。
假設溫度不變,則很多種物質會遵守歐姆定律,即這些物質所組成的物體,其電阻為常數,不跟電流或電壓有關,一般稱這些物質為「歐姆物質」;不遵守歐姆定律的物質為「非歐姆物質」。
在電路符號中,常以前綴R表示恆定電阻的電阻值,例如R1、R02、R100等。
導體與電阻器
像電線一類的物體,具有低電阻,可以很有效率地傳輸電流,這類物體稱為「導體」。通常導體是由像銅、金和銀一類具有優等導電性質的金屬製造,或者次等導電性質的鋁。電阻器是具有特定電阻的電路元件。製備電阻器所使用的原料有很多種;應該使用哪種原料,要視指定的電阻、能量耗散、準確度和成本等因素而定。
直流電
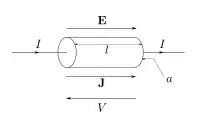
在物理學裏,對於物質的微觀層次電性質研究,會使用到的歐姆定律,以向量方程式表達為
- ;
在導體內任意兩點g、h,定義電壓為將單位電荷從點g移動到點h,電場力所需做的機械功[1]:
- ;
其中,是電壓,是機械功,是電荷量,是微小線元素。
假設,沿著積分路徑,電流密度為均勻電流密度,並且平行於微小線元素:
- ;
其中,是積分路徑的單位向量。
那麼,可以得到電壓:
- ;
其中,是積分路徑的徑長。
假設導體具有均勻的電阻率,則通過導體的電流密度也是均勻的:
- ;
其中,是導體的截面面積。
電壓簡寫為。電壓與電流成正比:
- 。
總結,電阻與電阻率的關係為
- 。
假設,則;將單位電荷從點g移動到點h,電場力需要作的機械功。所以,點g的電勢比點h的電勢高,從點g到點h的電勢差為。從點g到點h,電壓降是;從點h到點g,電壓升是。
交流電
假設電線傳導的電流是高頻率交流電,則由於趨膚效應,電線的有效截面面積會減小。假設平行排列幾條電線在一起,則由於鄰近效應,每一條電線的有效電阻會大於單獨電線的電阻。對於普通家用交流電,由於頻率很低,這些效應非常微小,可以忽略這些效應。
測量電阻
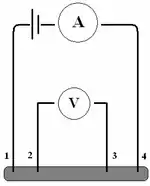
電阻計是測量電阻的儀器。由於探針電阻和接觸電阻會造成電壓降,簡單電阻器不能準確地測量低電阻。高準確度測量工作必須使用四端点测量技术()。
各種不同材料的電阻
金属
金属是一群原子以晶格結構形成的晶體,每個原子都擁有一层(或多层)由电子組成的外殼。處於外殼的电子能脫离原子核的吸引力而到处流动,形成一片電子海,使得金属能夠導电。當施加电勢差(即电压)於金屬兩端時,因為感受到电场的影响,這些自由电子會呈加速運動。但是每當自由電子與晶格發生碰撞,其動能會遭受損失,以熱能的形式將能量釋放,所以,電子的平均移動速度是漂移速度,其方向與電場方向相反。由於漂移運動,會產生電流。在现实中,物质的原子排列不可能為完全规则,因此电子在流动途中會被不按規则排列的原子散射,這是电阻的來源。
給予一個具有完美晶格的金屬晶體,移動於這晶體的電子,其運動等價於移動於自由空間、具有有效質量的電子的運動。所以,假設熱運動足夠微小,週期性結構沒有偏差,則這晶體的電阻等於零。但是,真實晶體並不完美,時常會出現晶體缺陷,有些晶格點的原子可能不存在,可能會被雜質侵佔。這樣,晶格的週期性會被擾動,因而電子會被散射。另外,假設溫度大於絕對零度,則處於晶格點的原子會發生熱震動,因而出現熱震動的粒子——聲子——移動於晶體。溫度越高,聲子越多。聲子會與電子發生碰撞,這過程稱為晶格散射()。主要由於上述兩種散射,自由電子的流動會被阻礙,晶體因此具有有限電阻[2]。
半導體和絕緣體
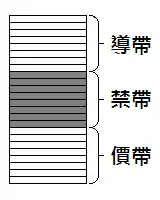
對於金屬,費米能級的位置在導帶區域內,因此金屬內部會出現自由的傳導電子。可是,對於半導體,費米能級的位置在能隙區域內。
本征半導體是未被摻雜的半導體,其費米能級大約為導帶最低值與價帶最高值的平均值。當溫度為絕對零度時,本征半導體內部沒有自由的傳導電子,電阻為無窮大。當溫度開始上升,高於絕對零度時,有些電子可能會獲得能量而進入傳導帶中;假設施加外電場,則這些電子在獲得外電場的能量後,會移動於金屬內部,因而形成電流。
雜質半導體是經過摻雜的半導體。靠著捐贈電子給導帶,或價帶接受空穴,外質半導體內部的雜質原子能夠增加電荷載子的密度,從而減低電阻。高度滲雜的半導體的導電性質類似金屬。在非常高溫度狀況,熱生成電荷載子的貢獻會超過雜質原子的貢獻;隨著溫度的增加,電阻會呈指數遞減。
非歐姆元件
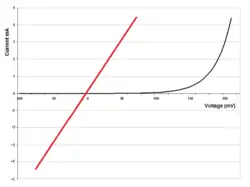
有些電路元件不遵守歐姆定律,它們的電壓與電流之間的關係(I-V線)乃非線性關係。PN接面二極體是一個顯明範例。如右圖所示,隨著二極體兩端電壓的遞增,電流並沒有線性遞增。給定外電壓,可以用I-V線來估計電流,而不能用歐姆定律來計算電流,因為電阻會因為電壓的不同而改變。具有這種特性的電阻或元件稱為「非線性電阻」或「非歐姆元件」。
非歐姆元件的常見實例包括二極體、氣體放電燈(螢光燈)、壓敏電阻等。
對於這類元件在特定電壓電流下的電阻量,使用V-I線的斜率(或是I-V曲線斜率的倒數),稱為小信號電阻()、增量電阻()或動態電阻(),定義為
- ,
溫度對電阻的影響
溫度对不同物质的电阻会有不同的影响。
導电体
- ;
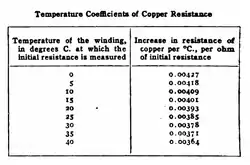
其中,是典型金屬在參考溫度為時的參考電阻,是電阻溫度係數。
是電阻變化百分比每單位溫度。每一種物質都有其特定的。實際而言,上述關係式只是近似,真實的物理是非線性的;換句話說,本身會隨著溫度的改變而變化。因此,通常會在字尾添加測量時的溫度。例如,是在溫度為15 °C時測量的電阻溫度係數;使用為電阻溫度係數,則參考溫度為15 °C,參考電阻為金屬在參考溫度為15 °C時的參考電阻,而且上述關係式只適用於計算溫度在15 °C附近的電阻 [6]。
稍加排列,這方程式又可表示為
- 。
取的極限,則可得到微分方程式[4]
- 。
所以,在溫度為時,物質的電阻溫度係數是,其電阻對溫度的曲線在溫度為時的斜率,除以溫度為時的電阻。
於1860年代,奧古斯土·馬西森想出馬西森定則()。這定則表明,總電阻率可以分為兩個項目[7]:
- ;
其中,是由於晶體缺陷而產生的電阻率,是由於聲子而產生的電阻率。
與金屬內部的缺陷密度有關,是電阻率對溫度的曲線外推至0K時的電阻率。因此,與溫度無關。等於。假若缺陷密度不高,則通常與缺陷密度無關。與電子跟聲子的碰撞率有關,而碰撞率與聲子密度成正比。假設溫度高於德拜溫度,則聲子密度與溫度成正比,所以,與溫度成正比:
- 、
- ;
其中,是比例常數。
這方程式等價於前面電阻與溫度的關係方程式。
假設溫度低於德拜溫度,則電阻與溫度的5次方成正比[8][9][10]:
- ;
其中,是比例常數。
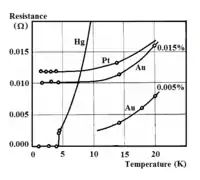
如右圖所示,當溫度接近絕對溫度時,黃金和白金的電阻趨向於常數;而當溫度小於4.2K時,水銀的電阻突然從0.002歐姆陡降為10-6歐姆,成為超導體。
半導体
溫度越高,本征半導體的導電性質越優良,電子會被熱能撞跳至導帶,從而可以自由的移動,也因而留下電洞於價帶,也可以自由的移動於價帶。這電阻行為以方程式表達為
- ;
其中,,是常數。
外質半導體的電阻對於溫度的反應比較複雜。從絕對零度開始,隨著溫度增加,由於載子迅速地離開施主或受主,電阻會急劇降低。當大多數的施主或受主都失去了載子之後,电阻会因載子的遷移率()下降而隨溫度稍为上升。当溫度升得更高,外質半導體的電阻行為類似本征半導體;施主或受主的載子數量超小於因熱能而產生的載子的數量,於是电阻会再度下降[12]。
绝缘体和电解质
绝缘体和电解质的电阻與溫度一般成非線性關係,而且不同物质有不同的變化,故不在此列出概括性的算式。
超导体
某些材料在温度接近绝对零度(-273.15°C)或极低的温度时会出现超导现象,目前发现的超导体的最高温度约是203开尔文(-70°C)。
應變對電阻的影響
導體的電阻受應變影響而改變。假設施加張力(一種應力的形式,會引起應變,即導體伸長)於導體,則導體沿張力的方向,其長度會增加,相對而言,導體於垂直張力方向的截面面積會減少。這兩種效應共同貢獻,使得受到張力的導體,其電阻會隨之增加。假設施加壓力,則由於壓縮(方向相反的應變:導體縮短,截面面積增加),導體應變部分的電阻會減少。應用這效應,應變片()可以測量物體的應變與所受張力。
參看
- 電測量()
- 熱阻()
- 薄膜電阻
- 量子霍爾效應,一種新的電阻測量標準。
- 近藤效應
- 四端点测量技术
參考文獻
- Alexander, Charles; Sadiku, Matthew, 3, revised, McGraw-Hill: pp. 9–10, 2006, ISBN 9780073301150
- Seymour J, Physical Electronics, pp 48–49, Pitman, 1972
- Horowitz, Paul; Winfield Hill. 2nd. Cambridge University Press. 1989: 13. ISBN 0-521-37095-7.
- Pender, Harold & Del Mar, William (编), 2nd, New York: John Wiley & Sons, Inc.: pp. 1350, 2094, 1922
- Bird, John, , Newnes: pp. 22–24, 2006, ISBN 9780750685566
- Ward, MR, Electrical Engineering Science, pp36–40, McGraw-Hill, 1971.
- Kittel, Charles, 8th, John Wiley & Sons, Inc.: 148–152, 2005, ISBN 9780471415268
- A. Matthiessen, Rep. Brit. Ass. 32, 144 (1862)
- A. Matthiessen, Progg. Anallen, 122, 47 (1864)
- Enss, Christian; Hunklinger, Siegfried, illustrated, Springer: pp. 216–218, 2005, ISBN 9783540231646
- 昂內斯, 海克, (PDF), Nobel Lecture, 1913年12月 [2010-12-23], (原始内容存档 (PDF)于2006-04-25)
- Seymour J, Physical Electronics, chapter 2, Pitman, 1972
外部連結
- 克萊門森大學車輛電子實驗室網頁:電阻計算機(英文)