Maple
MAPLE是一個符號運算和數值計算軟體平臺
| 開發者 | Waterloo Maple Inc. (Maplesoft)枫软 |
|---|---|
| 首次发布 | 1982年 |
| 当前版本 |
|
| 编程语言 | C语言, Java, Maple language |
| 操作系统 | 跨平台 |
| 类型 | 计算机代数系统 |
| 许可协议 | 私有 |
| 网站 | www.maplesoft.com/products/maple/ |
總覽
核心功能
用戶能够直接使用傳統數學符號进行輸入,也可以定制个性化的界面。对于数值计算有额外的支持,能够扩展到任意精度,同时亦支持符號演算及可视化。符號演算的例子参见下文。Maple内建有一种动态的命令行风格的编程语言,该语言支持具有作用域的变量。同时亦有其他語言的接口(C、FORTRAN、Java、Matlab和Visual Basic)。还具有与Excel进行交互的接口。
版本
| 版本 | 年份 |
|---|---|
| Maple 1.0 | 1982年1月 |
| Maple 1.1 | 1982年 |
| Maple 2.0 | 1982年5月 |
| Maple 2.1 | 1982年6月 |
| Maple 2.15 | 1982年8月 |
| Maple 2.2 | 1982年12月 |
| Maple 3.0 | 1983年5月 |
| Maple 3.1 | 1983年10月 |
| Maple 3.2 | 1984年4月 |
| Maple 3.3 | 1985年3月(第一個公開版本) |
| Maple 4.0 | 1986年4月 |
| Maple 4.1 | 1987年5月 |
| Maple 4.2 | 1987年12月 |
| Maple 4.3 | 1989年3月 |
| Maple V | 1990年8月 |
| Maple V R2 | 1992年11月 |
| Maple V R3 | 1994年3月15日 |
| Maple V R4 | 1996年1月 |
| Maple V R5 | 1997年11月1日 |
| Maple 6 | 2000年1月31日 |
| Maple 6.01 | ?年?月 |
| Maple 6.02 | ?年?月 |
| Maple 7.00 | 2001年5月28日 |
| Maple 7.01 | ?年?月 |
| Maple 8.00 | 2002年4月22日 |
| Maple 9.00 | 2003年6月30日 |
| Maple 9.01 | 2003年7月10日 |
| Maple 9.02 | 2003年?月 |
| Maple 9.03 | 2003年11月5日 |
| Maple 9.50 | 2004年4月7日 |
| Maple 9.51 | 2004年8月17日 |
| Maple 9.52 | 2005年1月21日 |
| Maple 10 | 2005年5月13日 |
| Maple 10.01 | 2005年?月 |
| Maple 10.02 | 2005年11月8日 |
| Maple 10.03 | ?年?月 |
| Maple 10.04 | 2006年5月30日 |
| Maple 10.05 | 2006年6月9日 |
| Maple 10.06 | 2006年10月2日 |
| Maple 11.0 | 2007年2月17日 |
| Maple 11.01 | 2007年7月10日 |
| Maple 11.02 | 2007年11月10日 |
| Maple 12.0 | 2008年4月10日 |
| Maple 12.01 | 2008年10月 |
| Maple 12.02 | 2008年12月 |
| Maple 13.0 | 2009年4月13日 |
| Maple 13.01 | 2009年7月8日 |
| Maple 13.02 | 2009年7月8日 |
| Maple 14.00 | 2010年4月5日 |
| Maple 14.01 | 2010年10月28日 |
| Maple 15 | 2011年4月13日 |
| Maple 15.01 | 2011年6月2日 |
| Maple 16 | 2012年3月28日 |
| Maple 16.01 | 2012年5月16日/8月27日 |
| Maple 16.02 | 2012年11月18日 |
| Maple 17.00 | 2013年2月21日/3月13日/4月10日 |
| Maple 18.00 | 2014年3月6日 |
| Maple 18.01 | 2014年5月 |
| Maple 18.01a | 2014年7月 |
| Maple 18.02 | 2014年11月 |
| Maple 2015 | 2015年3月 |
| Maple 2015.1 | 2015年11月 |
| Maple 2016 | 2016年3月2日 |
| Maple 2016.1 | 2016年4月20日 |
| Maple 2016.1.a | 2016年4月27日 |
| Maple 2017 | 2017年5月25日 |
| Maple 2017.1 | 2017年6月28日 |
| Maple 2017.2 | 2017年8月2日 |
| Maple 2017.3 | 2017年10月3日 |
| Maple 2018.0 | 2018年3月21日 |
| Maple 2019.0 | 2019年3月14日 |
Maple代码示例
简单指令式程序的构造:
myfac := proc(n::nonnegint)
local out, i;
out := 1;
for i from 2 to n do
out := out * i
end do;
out
end proc;
一些简单的函数也可以使用直观的箭头表示法表示
myfac := n -> product( i, i=1..n );
开方
evalf[100](2^1/12)
1.059463094359295264561825294946341700779204317494185628559208431458761646063255722383768376863945569
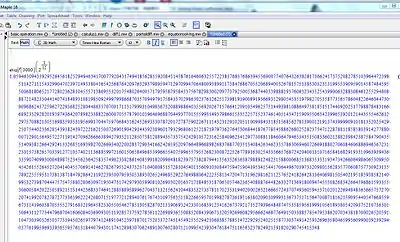
求根
f:=x^2-63*x+99=0;
solve(f,x);
,
f := x^7+3*x = 7;
solve(f,x);
- RootOf(, index = 1),
- RootOf(, index = 2),
- RootOf(, index = 3),
- RootOf(, index = 4),
- RootOf(, index = 5),
- RootOf(, index = 5),
- RootOf(, index =7),
evalf(%);
- (1.1922047171828134),
- (0.8658388666792263) + (0.9230818802764879) I,
- (0.2099602786426775) + (1.3442579297631496) I,
- (1.2519809466279554) + (0.6424819505558892) I,
- (1.2519809466279554) - (0.6424819505558892) I,
- (0.2099602786426775) - (1.3442579297631496) I,
- (0.8658388666792263) - (0.9230818802764879) I
f := sin(x)^3+5*cosh(x) = 0;
> solve(f, x);
RootOf(
> evalf(%);
- 0.2873691672 - 1.111497506 I
求解方程和不等式
根据,寻找的所有实数解。
solve({x-y > 6, (x+y)^5 = 9}, [x, y])[];
答案:
方程组
- 代数方程组
- > p1 := x*y*z-x*y^2-z-x-y; p2 := x*z-x^2-z-y+x; p3 := z^2-x^2-y^2;
- > sys := {p1, p2, p3};
- > var := {x, y, z};
- > solve(sys, var);
- {x = 0, y = y, z = -y}, {x = 3, y = 4, z = 5}, {x = 1, y = 0, z = -1}
- 三角方程组
- > f1 := cos(x)+sin(3*y)+tan(5*z) = 0;
- > f2 := cos(3*z)+tan(3*y^2)-sin(2*z^3) = 33;
- > f3 := tan(4*x+y)-sin(5*y-4*z) = 2*x;
- > sys1 := {f1, f2, f3};
- > var1 := {x, y, z};
- {x, y, z}
- > fsolve(sys1, var1);
- {x = -10.77771790, y = -2.397849343, z = -7.382158103}
矩阵与行列式
M:= Matrix([[1,2,3]], [a,b,c], [[x,y,z]]); # 矩阵样例
with(LinearAlgebra)
m:=Determinant(M);
答案:
- 朗斯基行列式
with(VectorCalculus);
w:=Wronskian([1,x,x^3+x-1],x)
Matrix(3, 3, {(1, 1) = 1, (1, 2) = x, (1, 3) = x^3+x-1, (2, 1) = 0, (2, 2) = 1, (2, 3) = 3*x^2+1, (3, 1) = 0, (3, 2) = 0, (3, 3) = 6*x})
d:=Determinant(w);
- 6x
- 雅可比矩阵
J := Jacobian([r*sin(t)), r^2*cosh(t)], [r, t]);
m:=Matrix(2, 2, {(1, 1) = cos(t), (1, 2) = -r*sin(t), (2, 1) = sinh(t), (2, 2) = r*cosh(t)})
d:=Determinant(m);
sin(t)*r^2*sinh(t)-2r^2cos(t)cosh(t)
f := x^3+y*cos(x)+t*tan(y))
with(VectorCalculus);
h:=hessian(f,[x,y,t]);
积分
求.
int(cos(x/a), x);
答案:
求.
int(sin(x/a), x);
答案:
注意:Maple在积分时不提供常数项C,必须自行补上。
- 定积分
> int(cos(x/a), x = 1 .. 5);
- 16 a sin(1/a)* cos^4(1/a) - 12 a sin^2(1/a)
求解线性微分方程
计算以下线性常微分方程的一个精确解初始条件为
dsolve( {diff(y(x),x,x) - 3*y(x) = x, y(0)=0, D(y)(0)=2}, y(x) );
答案:
非线性常微分方程
dsolve(diff(y(x), x, x) = x^2*y(x))
解:
- BesselI(,)
+BesselK(,)
级数展开
series(tanh(x),x=0,15)
f:=int(exp^cosh(x),x) series(f,x=0,15);
拉普拉斯变换
with(inttrans);
> f := (1+A*t+B*t^2)*exp(c*t);
> laplace(f, t, s);
- 反拉普拉斯变换
invlaplace(1/(s-a),s,x)
z := y(t);
- y(t)
- f := diff(z, t, t)+a*(diff(z, t)) = b*z;
with(inttrans);
- g := laplace(f, t, s);
- s^2*laplace(y(t), t, s) - D(y)(0) - s y(0)
- + a s^2 laplace(y(t), t, s) - a y(0) = b laplace(y(t), t, s)
- invlaplace(g, s, t);
傅里叶变换
with(inttrans);
fourier(sin(x),x,w)
*(Dirac(w-1)+Dirac(w+1))
绘制单变量函数图形
绘制函数,
plot(x*sin(x),x=-10..10);
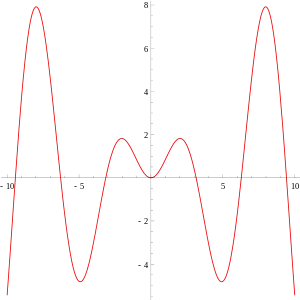
绘制双变量函数
绘制函数,和的范围为 -1到1
plot3d(x^2+y^2,x=-1..1,y=-1..1);
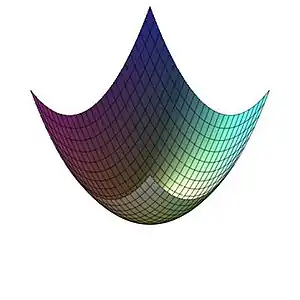
绘制函数动画
- 二维动画
with(plots);
animate(subs(k = .5, f), x = -30 .. 30, t = -10 .. 10, numpoints = 200, frames = 50, color = red, thickness = 3);
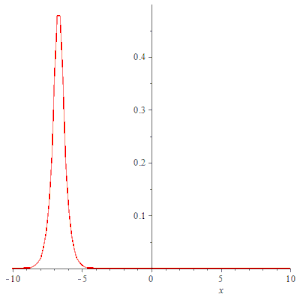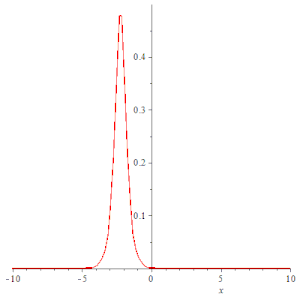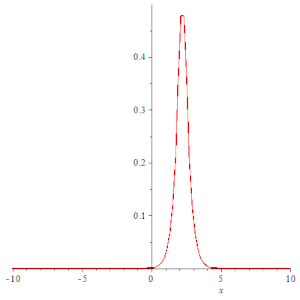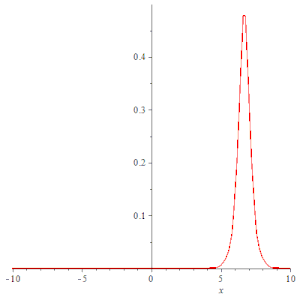 钟形孤立子 |
 三维函数动画 |
- 三维动画
with(plots)
animate3d(cos(t*x)*sin(3*t*y), x = -Pi .. Pi, y = -Pi .. Pi, t = 1 .. 2)
求解偏微分方程组
求解偏微分方程组
条件为.
eqn1:= diff(v(x, t), x) = -u(x,t)*v(x,t):
eqn2:= diff(v(x, t), t) = -v(x,t)*(diff(u(x,t), x))+v(x,t)*u(x,t)^2:
eqn3:= diff(u(x,t), t)+2*u(x,t)*(diff(u(x,t), x))-(diff(diff(u(x,t), x), x)) = 0:
pdsolve({eqn1,eqn2,eqn3,v(x,t)<>0},[u,v]): op(%);
答案:
积分方程
寻找函数满足积分方程
.
eqn:= f(x)-3*Integrate((x*y+x^2*y^2)*f(y), y=-1..1) = h(x): intsolve(eqn,f(x));
答案:
注释
- 现在,MATLAB已改用MuPAD替代了matlab的Maple符号计算内核。
参考文献
- 何青 王丽芬编著《Maple教程》 科学出版社 2010 ISBN 9787030177445
- David Betounes, Partial Differential Equations for Computational Science: With Maple and Vector Analysis Springer, 1998 ISBN 9780387983004
- George Articolo Partial Differential Equations & Boundary Value Problems with Maple V Academic Press 1998 ISBN 9780120644759