In order theory, a branch of mathematics, the 1/3–2/3 conjecture states that, if one is comparison sorting a set of items then, no matter what comparisons may have already been performed, it is always possible to choose the next comparison in such a way that it will reduce the number of possible sorted orders by a factor of 2/3 or better. Equivalently, in every finite partially ordered set that is not totally ordered, there exists a pair of elements x and y with the property that at least 1/3 and at most 2/3 of the linear extensions of the partial order place x earlier than y.
Example
The partial order formed by three elements a, b, and c with a single comparability relationship, a ≤ b, has three linear extensions, a ≤ b ≤ c, a ≤ c ≤ b, and c ≤ a ≤ b. In all three of these extensions, a is earlier than b. However, a is earlier than c in only two of them, and later than c in the third. Therefore, the pair of a and c have the desired property, showing that this partial order obeys the 1/3–2/3 conjecture.
This example shows that the constants 1/3 and 2/3 in the conjecture are tight; if q is any fraction strictly between 1/3 and 2/3, then there would not exist a pair x, y in which x is earlier than y in a number of partial orderings that is between q and 1 − q times the total number of partial orderings.[1]
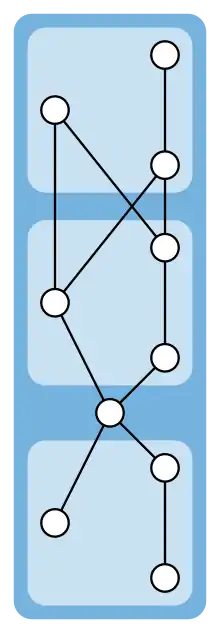
More generally, let P be any series composition of three-element partial orders and of one-element partial orders, such as the one in the figure. Then P forms an extreme case for the 1/3–2/3 conjecture in the sense that, for each pair x, y of elements, one of the two elements occurs earlier than the other in at most 1/3 of the linear extensions of P. Partial orders with this structure are necessarily series-parallel semiorders; they are the only known extreme cases for the conjecture and can be proven to be the only extreme cases with width two.[2]
Definitions
A partially ordered set is a set X together with a binary relation ≤ that is reflexive, antisymmetric, and transitive. A total order is a partial order in which every pair of elements is comparable. A linear extension of a finite partial order is a sequential ordering of the elements of X, with the property that if x ≤ y in the partial order, then x must come before y in the linear extension. In other words, it is a total order compatible with the partial order. If a finite partially ordered set is totally ordered, then it has only one linear extension, but otherwise it will have more than one. The 1/3–2/3 conjecture states that one can choose two elements x and y such that, among this set of possible linear extensions, between 1/3 and 2/3 of them place x earlier than y, and symmetrically between 1/3 and 2/3 of them place y earlier than x.[3]
There is an alternative and equivalent statement of the 1/3–2/3 conjecture in the language of probability theory. One may define a uniform probability distribution on the linear extensions in which each possible linear extension is equally likely to be chosen. The 1/3–2/3 conjecture states that, under this probability distribution, there exists a pair of elements x and y such that the probability that x is earlier than y in a random linear extension is between 1/3 and 2/3.[3]
In 1984, Jeff Kahn and Michael Saks defined δ(P), for any partially ordered set P, to be the largest real number δ such that P has a pair x, y with x earlier than y in a number of linear extensions that is between δ and 1 − δ of the total number of linear extensions. In this notation, the 1/3–2/3 conjecture states that every finite partial order that is not total has δ(P) ≥ 1/3.[4]
History
The 1/3–2/3 conjecture was formulated by Sergey Kislitsyn in 1968,[5] and later made independently by Michael Fredman[6] and by Nati Linial in 1984.[3] It was listed as a featured unsolved problem at the founding of the journal Order, and remains unsolved; being called "one of the most intriguing problems in the combinatorial theory of posets."[3]
A survey of the conjecture was produced in 1999.[7]
Partial results
The 1/3–2/3 conjecture is known to be true for certain special classes of partial orders, including partial orders of width two,[8] partial orders of height two,[9] partial orders with at most 11 elements,[10] partial orders in which each element is incomparable to at most six others,[11] series-parallel partial orders,[12] semiorders.[13] and polytrees.[14] In the limit as n goes to infinity, the proportion of n-element partial orders that obey the 1/3–2/3 conjecture approaches 100%.[10]
In 1995, Graham Brightwell, Stefan Felsner, and William Trotter proved that, for any finite partial order P that is not total, δ(P) ≥ 1/2 − √5/10 ≈ 0.276. Their results improve previous weaker bounds of the same type.[15] They use the probabilistic interpretation of δ(P) to extend its definition to certain infinite partial orders; in that context, they show that their bounds are optimal, in that there exist infinite partial orders with δ(P) = 1/2 − √5/10.
Applications
In 1984 Jeff Kahn and Saks proposed the following application for the problem: suppose one wishes to comparison sort a totally ordered set X, for which some partial order information is already known in the form of a partial order on X. In the worst case, each additional comparison between a pair x and y of elements may yield as little information as possible, by resolving the comparison in a way that leaves as many linear extensions as possible compatible with the comparison result. The 1/3–2/3 conjecture states that, at each step, one may choose a comparison to perform that reduces the remaining number of linear extensions by a factor of 2/3; therefore, if there are E linear extensions of the partial order given by the initial information, the sorting problem can be completed in at most log3/2E additional comparisons.[4]
However, this analysis neglects the complexity of selecting the optimal pair x and y to compare. Additionally, it may be possible to sort a partial order using a number of comparisons that is better than this analysis would suggest, because it may not be possible for this worst-case behavior to occur at each step of a sorting algorithm. In this direction, it has been conjectured that logφE comparisons may suffice, where φ denotes the golden ratio.[10]
A closely related class of comparison sorting problems was considered by Fredman in 1976, among them the problem of comparison sorting a set X when the sorted order of X is known to lie in some set S of permutations of X. Here S is not necessarily generated as the set of linear extensions of a partial order. Despite this added generality, Fredman showed that X can be sorted using log2|S| + O(|X|) comparisons, expressed in big O notation. This same bound applies as well to the case of partial orders and shows that log2E + O(n) comparisons suffice.[16]
Generalizations and related results
In 1984, Kahn and Saks conjectured that, in the limit as w tends to infinity, the value of δ(P) for partially ordered sets of width w should tend to 1/2. In particular, they expect that only partially ordered sets of width two can achieve the worst case value δ(P) = 1/3,[17] and in 1985 Martin Aigner stated this explicitly as a conjecture.[2] The smallest known value of δ(P) for posets of width three is 14/39,[18] and computer searches have shown that no smaller value is possible for width-3 posets with nine or fewer elements.[9] Another related conjecture, again based on computer searches, states that there is a gap between 1/3 and the other possible values of δ(P): whenever a partial order does not have δ(P) exactly 1/3, it has δ(P) ≥ 0.348843.[19]
Marcin Peczarski[10][11] has formulated a "gold partition conjecture" stating that in each partial order that is not a total order one can find two consecutive comparisons such that, if ti denotes the number of linear extensions remaining after i of the comparisons have been made, then (in each of the four possible outcomes of the comparisons) t0 ≥ t1 + t2. If this conjecture is true, it would imply the 1/3–2/3 conjecture: the first of the two comparisons must be between a pair that splits the remaining comparisons by at worst a 1/3–2/3 ratio. The gold partition conjecture would also imply that a partial order with E linear extensions can be sorted in at most logφE comparisons; the name of the conjecture is derived from this connection with the golden ratio.
It is #P-complete, given a finite partial order P and a pair of elements x and y, to calculate the proportion of the linear extensions of P that place x earlier than y.[20]
Notes
- ↑ Kahn & Saks (1984); Brightwell, Felsner & Trotter (1995).
- 1 2 Aigner (1985).
- 1 2 3 4 Brightwell, Felsner & Trotter (1995).
- 1 2 Kahn & Saks (1984)
- ↑ Kislitsyn (1968)
- ↑ However, despite the close connection of Fredman (1976) to the problem of sorting partially ordered data and hence to the 1/3–2/3 conjecture, it is not mentioned in that paper.
- ↑ Brightwell (1999)
- ↑ Linial (1984), Theorem 2; Sah (2021).
- 1 2 Trotter, Gehrlein & Fishburn (1992).
- 1 2 3 4 Peczarski (2006).
- 1 2 Peczarski (2008).
- ↑ Zaguia (2012).
- ↑ Brightwell (1989).
- ↑ Zaguia (2019).
- ↑ Brightwell, Felsner & Trotter (1995); Kahn & Saks (1984); Khachiyan (1989); Kahn & Linial (1991); Felsner & Trotter (1993).
- ↑ Fredman (1976)
- ↑ Kahn & Saks (1984).
- ↑ Saks (1985).
- ↑ Peczarski (2019).
- ↑ Brightwell & Winkler (1991).
References
- Aigner, Martin (1985), "A note on merging", Order, 2 (3): 257–264, doi:10.1007/BF00333131, S2CID 118877843.
- Brightwell, Graham R. (1989), "Semiorders and the 1/3–2/3 conjecture", Order, 5 (4): 369–380, doi:10.1007/BF00353656, S2CID 86860160.
- Brightwell, Graham R. (1999), "Balanced pairs in partial orders", Discrete Mathematics, 201 (1–3): 25–52, doi:10.1016/S0012-365X(98)00311-2.
- Brightwell, Graham R.; Felsner, Stefan; Trotter, William T. (1995), "Balancing pairs and the cross product conjecture", Order, 12 (4): 327–349, CiteSeerX 10.1.1.38.7841, doi:10.1007/BF01110378, MR 1368815, S2CID 14793475.
- Brightwell, Graham R.; Winkler, Peter (1991), "Counting linear extensions", Order, 8 (3): 225–242, doi:10.1007/BF00383444, S2CID 119697949.
- Felsner, Stefan; Trotter, William T. (1993), "Balancing pairs in partially ordered sets", Combinatorics, Paul Erdős is eighty, Bolyai Society Mathematical Studies, vol. 1, Budapest: János Bolyai Mathematical Society, pp. 145–157, MR 1249709.
- Fredman, M. L. (1976), "How good is the information theory bound in sorting?", Theoretical Computer Science, 1 (4): 355–361, doi:10.1016/0304-3975(76)90078-5
- Kahn, Jeff; Linial, Nati (1991), "Balancing extensions via Brunn-Minkowski", Combinatorica, 11 (4): 363–368, doi:10.1007/BF01275670, S2CID 206793172.
- Kahn, Jeff; Saks, Michael (1984), "Balancing poset extensions", Order, 1 (2): 113–126, doi:10.1007/BF00565647, S2CID 123370506.
- Khachiyan, Leonid (1989), "Optimal algorithms in convex programming decomposition and sorting", in Jaravlev, J. (ed.), Computers and Decision Problems (in Russian), Moscow: Nauka, pp. 161–205. As cited by Brightwell, Felsner & Trotter (1995).
- Kislitsyn, S. S. (1968), "A finite partially ordered set and its corresponding set of permutations", Mathematical Notes, 4 (5): 798–801, doi:10.1007/BF01111312, S2CID 120228193.
- Linial, Nati (1984), "The information-theoretic bound is good for merging", SIAM Journal on Computing, 13 (4): 795–801, doi:10.1137/0213049, S2CID 5149351.
- Peczarski, Marcin (2006), "The gold partition conjecture", Order, 23 (1): 89–95, doi:10.1007/s11083-006-9033-1, S2CID 42415160.
- Peczarski, Marcin (2008), "The gold partition conjecture for 6-thin posets", Order, 25 (2): 91–103, doi:10.1007/s11083-008-9081-9, S2CID 42034095.
- Peczarski, Marcin (2019), "The worst balanced partially ordered sets—ladders with broken rungs", Experimental Mathematics, 28 (2): 181–184, doi:10.1080/10586458.2017.1368050, MR 3955809, S2CID 125593629.
- Sah, Ashwin (2021), "Improving the – conjecture for width two posets", Combinatorica, 41 (1): 99–126, arXiv:1811.01500, doi:10.1007/s00493-020-4091-3, MR 4235316, S2CID 119604901
- Saks, Michael (1985), "Balancing linear extensions of ordered sets", Unsolved problems, Order, 2: 327–330, doi:10.1007/BF00333138, S2CID 189901558
- Trotter, William T.; Gehrlein, William V.; Fishburn, Peter C. (1992), "Balance theorems for height-2 posets", Order, 9 (1): 43–53, doi:10.1007/BF00419038, S2CID 16157076.
- Zaguia, Imed (2012), "The 1/3-2/3 Conjecture for N-free ordered sets", Electronic Journal of Combinatorics, 19 (2): P29, arXiv:1107.5626, Bibcode:2011arXiv1107.5626Z, doi:10.37236/2345, S2CID 1979845.
- Zaguia, Imed (2019), "The 1/3–2/3 conjecture for ordered sets whose cover graph is a forest", Order, 36 (2): 335–347, arXiv:1610.00809, doi:10.1007/s11083-018-9469-0, MR 3983482, S2CID 119631612.