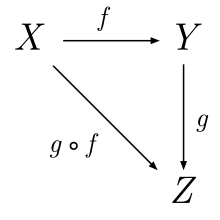In mathematics, specifically, in category theory, a 2-functor is a morphism between 2-categories.[1] They may be defined formally using enrichment by saying that a 2-category is exactly a Cat-enriched category and a 2-functor is a Cat-functor.[2]
Explicitly, if C and D are 2-categories then a 2-functor consists of
- a function , and
- for each pair of objects , a functor
such that each strictly preserves identity objects and they commute with horizontal composition in C and D.
See [3] for more details and for lax versions.
References
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.