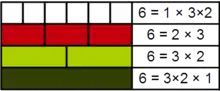
Demonstration, with Cuisenaire rods, of the 2-almost prime nature of the number 6

In number theory, a natural number is called k-almost prime if it has k prime factors.^[1][2][3] More formally, a number n is k-almost prime if and only if Ω(n) = k, where Ω(n) is the total number of primes in the prime factorization of n (can be also seen as the sum of all the primes' exponents):

${\displaystyle \Omega (n):=\sum a_{i}\qquad {\mbox{if}}\qquad n=\prod p_{i}^{a_{i}}.}$

A natural number is thus prime if and only if it is 1-almost prime, and semiprime if and only if it is 2-almost prime. The set of k-almost primes is usually denoted by P_k. The smallest k-almost prime is 2^k. The first few k-almost primes are:

The number π_k(n) of positive integers less than or equal to n with exactly k prime divisors (not necessarily distinct) is asymptotic to:^[4]

${\displaystyle \pi _{k}(n)\sim \left({\frac {n}{\log n}}\right){\frac {(\log \log n)^{k-1}}{(k-1)!}},}$

a result of Landau.^[5] See also the Hardy–Ramanujan theorem.

Properties

• The multiple of a ${\displaystyle k_{1}}$-almost prime and a ${\displaystyle k_{2}}$-almost prime is a ${\displaystyle (k_{1}+k_{2})}$-almost prime.
• A ${\displaystyle k}$-almost prime cannot have a ${\displaystyle n}$-almost prime as a factor for all ${\displaystyle n>k}$.

References

External links

• Weisstein, Eric W. "Almost prime". MathWorld.