In triangle geometry, the Bernoulli quadrisection problem asks how to divide a given triangle into four equal-area pieces by two perpendicular lines. Its solution by Jacob Bernoulli was published in 1687.[1][2] Leonhard Euler formulated a complete solution in 1779.[1][3]
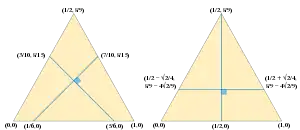
As Euler proved, in a scalene triangle, it is possible to find a subdivision of this form so that two of the four crossings of the lines and the triangle lie on the middle edge of the triangle, cutting off a triangular area from that edge and leaving the other three areas as quadrilaterals.[1][3] It is also possible for some triangles to be subdivided differently, with two crossings on the shortest of the three edges; however, it is never possible for two crossings to lie on the longest edge. Among isosceles triangles, the one whose height at its apex is 8/9 of its base length is the only one with exactly two perpendicular quadrisections. One of the two uses the symmetry axis as one of the two perpendicular lines, while the other has two lines of slope , each crossing the base and one side.[1]
This subdivision of a triangle is a special case of a theorem of Richard Courant and Herbert Robbins that any plane area can be subdivided into four equal parts by two perpendicular lines, a result that is related to the ham sandwich theorem.[4] Although the triangle quadrisection has a solution involving the roots of low-degree polynomials,[1] the more general quadrisection of Courant and Robbins can be significantly more difficult: for any computable number there exist convex shapes whose boundaries can be accurately approximated to within any desired error in polynomial time, with a unique perpendicular quadrisection whose construction computes .[5]
In 2022, the first place in an Irish secondary school science competition, the Young Scientist and Technology Exhibition, went to a project by Aditya Joshi and Aditya Kumar using metaheuristic methods to find numerical solutions to the Bernoulli quadrisection problem.[6]
Notes and references
- 1 2 3 4 5 6 Eberhart, Carl (2018), "Revisiting the quadrisection problem of Jacob Bernoulli" (PDF), Forum Geometricorum, 18: 7–16, arXiv:1611.06658, MR 3755894
- ↑ Bernoulli, Jakob; Battier, Jean Jacques (1744), "XXIX: Solutio algebraica problematis de quadrisectione trianguli scaleni, per duas normales rectas", Jacobi Bernoulli, Basileensis, Opera (in Latin), Sumptibus Hæredum Cramer & Fratrum Philibert, pp. 228–335, doi:10.3931/E-RARA-3584
- 1 2 Euler, Leonhard (1779), "Solutio completa problematis de quadrisectione trianguli per duas rectas inter se normales", Mémoires de l'académie des sciences de St.-Petersbourg (in Latin), 1: 49–87
- ↑ Courant, Richard; Robbins, Herbert (1941), "6.1. Some applications of Bolzano's theorem: Geometrical applications", What Is Mathematics?, New York: Oxford University Press, pp. 317–319, MR 0005358
- ↑ Yu, Fuxiang (2007), "On the complexity of the pancake problem", Mathematical Logic Quarterly, 53 (4–5): 532–546, doi:10.1002/malq.200710016, MR 2351948
- ↑ El-Hassany, Reem (January 15, 2022), Dublin students take top prize at BT Young Scientist, Raidió Teilifís Éireann