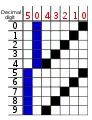
Bi-quinary coded decimal is a numeral encoding scheme used in many abacuses and in some early computers, including the Colossus.[2] The term bi-quinary indicates that the code comprises both a two-state (bi) and a five-state (quinary) component. The encoding resembles that used by many abacuses, with four beads indicating the five values either from 0 through 4 or from 5 through 9 and another bead indicating which of those ranges (which can alternatively be thought of as +5).
Several human languages, most notably Fula and Wolof also use biquinary systems. For example, the Fula word for 6, jowi e go'o, literally means five [plus] one. Roman numerals use a symbolic, rather than positional, bi-quinary base, even though Latin is completely decimal.
The Korean finger counting system Chisanbop uses a bi-quinary system, where each finger represents a one and a thumb represents a five, allowing one to count from 0 to 99 with two hands.
One advantage of one bi-quinary encoding scheme on digital computers is that it must have 2 bits set (one in the binary field and one in the quinary field), providing a built in checksum to verify if the number is valid or not. (Stuck bits happened frequently with computers using mechanical relays.)
Examples
Several different representations of bi-quinary coded decimal have been used by different machines. The two-state component is encoded as one or two bits, and the five-state component is encoded using three to five bits. Some examples are:
- Roman and Chinese abacuses
- Stibitz[3] relay calculators at Bell Labs from Model II onwards
- FACOM 128 relay calculators at Fujitsu
- IBM 650 – seven bits
- Two bi bits: 0 5 and five quinary bits: 0 1 2 3 4, with error checking.
- Exactly one bi bit and one quinary bit is set in a valid digit. In the pictures of the front panel below and in close-up, the bi-quinary encoding of the internal workings of the machine are evident in the arrangement of the lights – the bi bits form the top of a T for each digit, and the quinary bits form the vertical stem.
- (the machine was running when the photograph was taken and the active bits are visible in the close-up and just discernible in the full panel picture)
| Value | 05-01234 bits[1] |  IBM 650 front panel  Close-up of IBM 650 indicators |
| 0 | 10-10000 | |
| 1 | 10-01000 | |
| 2 | 10-00100 | |
| 3 | 10-00010 | |
| 4 | 10-00001 | |
| 5 | 01-10000 | |
| 6 | 01-01000 | |
| 7 | 01-00100 | |
| 8 | 01-00010 | |
| 9 | 01-00001 |
- Remington Rand 409 - five bits
- One quinary bit (tube) for each of 1, 3, 5, and 7 - only one of these would be on at the time.
- The fifth bi bit represented 9 if none of the others were on; otherwise it added 1 to the value represented by the other quinary bit.
- (sold in the two models UNIVAC 60 and UNIVAC 120)
| Value | 1357-9 bits |
| 0 | 0000-0 |
| 1 | 1000-0 |
| 2 | 1000-1 |
| 3 | 0100-0 |
| 4 | 0100-1 |
| 5 | 0010-0 |
| 6 | 0010-1 |
| 7 | 0001-0 |
| 8 | 0001-1 |
| 9 | 0000-1 |
- UNIVAC Solid State – four bits
| Value | p-5-421 bits |
| 0 | 1-0-000 |
| 1 | 0-0-001 |
| 2 | 0-0-010 |
| 3 | 1-0-011 |
| 4 | 0-0-100 |
| 5 | 0-1-000 |
| 6 | 1-1-001 |
| 7 | 1-1-010 |
| 8 | 0-1-011 |
| 9 | 1-1-100 |
- UNIVAC LARC – four bits[9]
- One bi bit: 5, three Johnson counter-coded quinary bits and one parity check bit
| Value | p-5-qqq bits |
| 0 | 1-0-000 |
| 1 | 0-0-001 |
| 2 | 1-0-011 |
| 3 | 0-0-111 |
| 4 | 1-0-110 |
| 5 | 0-1-000 |
| 6 | 1-1-001 |
| 7 | 0-1-011 |
| 8 | 1-1-111 |
| 9 | 0-1-110 |
See also
References
- 1 2 Ledley, Robert Steven; Rotolo, Louis S.; Wilson, James Bruce (1960). "Part 4. Logical Design of Digital-Computer Circuitry; Chapter 15. Serial Arithmetic Operations; Chapter 15-7. Additional Topics". Digital Computer and Control Engineering (PDF). McGraw-Hill Electrical and Electronic Engineering Series (1 ed.). New York, US: McGraw-Hill Book Company, Inc. (printer: The Maple Press Company, York, Pennsylvania, US). pp. 517–518. ISBN 0-07036981-X. ISSN 2574-7916. LCCN 59015055. OCLC 1033638267. OL 5776493M. SBN 07036981-X. ISBN 978-0-07036981-8. ark:/13960/t72v3b312. Archived (PDF) from the original on 2021-02-19. Retrieved 2021-02-19. p. 518:
[…] The use of the biquinary code in this respect is typical. The binary part (i.e., the most significant bit) and the quinary part (the other 4 bits) are first added separately; then the quinary carry is added to the binary part. If a binary carry is generated, this is propagated to the quinary part of the next decimal digit to the left. […]
(xxiv+835+1 pages) - ↑ "Why Use Binary? - Computerphile". YouTube. 2015-12-04. Archived from the original on 2021-12-12. Retrieved 2020-12-10.
- ↑ Stibitz, George Robert; Larrivee, Jules A. (1957). Written at Underhill, Vermont, US. Mathematics and Computers (1 ed.). New York, US / Toronto, Canada / London, UK: McGraw-Hill Book Company, Inc. p. 105. LCCN 56-10331. (10+228 pages)
- ↑ Berger, Erich R. (1962). "1.3.3. Die Codierung von Zahlen". Written at Karlsruhe, Germany. In Steinbuch, Karl W. (ed.). Taschenbuch der Nachrichtenverarbeitung (in German) (1 ed.). Berlin / Göttingen / New York: Springer-Verlag OHG. pp. 68–75. LCCN 62-14511.
- ↑ Berger, Erich R.; Händler, Wolfgang (1967) [1962]. Steinbuch, Karl W.; Wagner, Siegfried W. (eds.). Taschenbuch der Nachrichtenverarbeitung (in German) (2 ed.). Berlin, Germany: Springer-Verlag OHG. LCCN 67-21079. Title No. 1036.
- ↑ Steinbuch, Karl W.; Weber, Wolfgang; Heinemann, Traute, eds. (1974) [1967]. Taschenbuch der Informatik - Band II - Struktur und Programmierung von EDV-Systemen (in German). Vol. 2 (3 ed.). Berlin, Germany: Springer-Verlag. ISBN 3-540-06241-6. LCCN 73-80607.
{{cite book}}:|work=ignored (help) - ↑ Dokter, Folkert; Steinhauer, Jürgen (1973-06-18). Digital Electronics. Philips Technical Library (PTL) / Macmillan Education (Reprint of 1st English ed.). Eindhoven, Netherlands: The Macmillan Press Ltd. / N. V. Philips' Gloeilampenfabrieken. doi:10.1007/978-1-349-01417-0. ISBN 978-1-349-01419-4. SBN 333-13360-9. Retrieved 2020-05-11. (270 pages) (NB. This is based on a translation of volume I of the two-volume German edition.)
- ↑ Dokter, Folkert; Steinhauer, Jürgen (1975) [1969]. Digitale Elektronik in der Meßtechnik und Datenverarbeitung: Theoretische Grundlagen und Schaltungstechnik. Philips Fachbücher (in German). Vol. I (improved and extended 5th ed.). Hamburg, Germany: Deutsche Philips GmbH. p. 50. ISBN 3-87145-272-6. (xii+327+3 pages) (NB. The German edition of volume I was published in 1969, 1971, two editions in 1972, and 1975. Volume II was published in 1970, 1972, 1973, and 1975.)
- 1 2 Savard, John J. G. (2018) [2006]. "Decimal Representations". quadibloc. Archived from the original on 2018-07-16. Retrieved 2018-07-16.
Further reading
- Military Handbook: Encoders - Shaft Angle To Digital (PDF). United States Department of Defense. 1991-09-30. MIL-HDBK-231A. Archived (PDF) from the original on 2020-07-25. Retrieved 2020-07-25. (NB. Supersedes MIL-HDBK-231(AS) (1970-07-01).)