A bitwise trie is a special form of trie where each node with its child-branches represents a bit sequence of one or more bits of a key. A bitwise trie with bitmap uses a bitmap to denote valid child branches.
Tries and bitwise tries
A trie is a type of search tree where – unlike for example a B-tree – keys are not stored in the nodes but in the path to leaves. The key is distributed across the tree structure. In a "classic" trie, each node with its child-branches represents one symbol of the alphabet of one position (character) of a key.
In bitwise tries, keys are treated as bit-sequence of some binary representation and each node with its child-branches represents the value of a sub-sequence of this bit-sequence to form a binary tree (the sub-sequence contains only one bit) or n-ary tree (the sub-sequence contains multiple bits).
To give an example that explains the difference between "classic" tries and bitwise tries: For numbers as keys, the alphabet for a trie could consist of the symbols '0' .. '9' to represent digits of a number in the decimal system and the nodes would have up to 10 possible children.
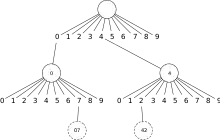
There are multiple straight forward approaches to implement such a trie as physical data structure. To state two:
- A node can be represented having an array of child pointers for each symbol of the alphabet – an array of 10 pointers per node in the decimal number example. This gives a lookup time with being the length of the key. But this isn't space efficient as each node preserves space for all possible child symbols even if there's no key that realizes that path.
- A node contains a list of (symbol, child pointer) tuples, ordered by symbol to allow a binary search through that list. This has a better space efficiency but the lookup time now is . An ideal trie has an access time that is independent of the amount of keys stored.
These approaches get worse for larger alphabets, if, for example, the key is a string of Unicode characters. Treating the key as bit-sequence allows to have a fixed cardinality per node.
Bitwise trie with bitmap
Bagwell[1] presented a time and space efficient solution for tries named Array Mapped Tree (AMT). The Hash array mapped trie (HAMT) is based on AMT. The compact trie node representation uses a bitmap to mark every valid branch – a bitwise trie with bitmap. The AMT uses eight 32-bit bitmaps per node to represent a 256-ary trie that is able to represent an 8 bit sequence per node. With 64-Bit-CPUs (64-bit computing) a variation is to have a 64-ary trie with only one 64-bit bitmap per node that is able to represent a 6 bit sequence.
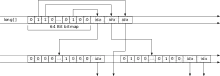
To determine the index of the child pointer of a node for such a given 6-bit value, the amount of preceding child pointers has to be calculated. It turns out that this can be implemented quite efficiently.
Node traversal
long bitMap = mem[nodeIdx];
long bitPos = 1L << value; // 6-bit-value
if ((bitMap & bitPos) == 0)
return false; // not found
long childNodeIdx = mem[nodeIdx + 1 + Long.bitCount(bitMap & (bitPos - 1))];
The offset to find the index based on the current node index is the amount of least significant bits set in the bitmap before the target position plus one for the bitmap. The amount of least significant bits set can be calculated efficiently with constant time complexity using simple bit operations and a CTPOP (count population) operation that determines the number of set bits, which is available as Long.bitCount() in Java. CTPOP itself can be implemented quite efficiently using a "bit-hack" [2] and many modern CPUs even provide CTPOP as a dedicated instruction treated by compilers as intrinsic function.
CTPOP bit-hack implementation
int bitCount(long x)
x -= ((i >>> 1) & 0x5555555555555555L);
x = (x & 0x3333333333333333L) + ((x >>> 2) & 0x3333333333333333L);
x = (x + (x >>> 4)) & 0x0f0f0f0f0f0f0f0fL;
x += (x >>> 8);
x += (x >>> 16);
x += (x >>> 32);
return x & 0x7f;
How to use this principle for an universal index for database and Information retrieval applications is described in.[3] A specialized and simplified solution demonstrating these concepts is shown below for an implementation of a 32-Bit-Integer set.
Set implementation example
Physical data structure
In this example implementation for a bitwise trie with bitmap, nodes are placed in an array of long (64-bit) integers. A node is identified by the position (index) in that array. The index of the root node marks the root of the trie.
Nodes are allocated from unused space in that array, extending the array if necessary. In addition, nodes, that are replaced, are collected in free lists and their space is recycled. Without this recycling, the data structure can be used to implement a persistent data structure by just keeping the previous root index and never overriding existing nodes but always creating a copy of a changed node.
Leaf nodes are inlined: Instead of having a child-pointer to a leaf node, the bitmap of the leaf node itself is stored.
public class BBTrieSet {
long[] mem;
long[] freeLists;
long freeIdx;
long root;
long count;
// maximum node size is 1 (bitMap) + 64 (child pointers or leaf values) + 1 as arrays are zero based
final static int FREE_LIST_SIZE = 1+64+1;
final static int KNOWN_EMPTY_NODE = 0;
final static int KNOWN_DELETED_NODE = 1;
final static int HEADER_SIZE = 2; // KNOWN_EMPTY_NODE, KNOWN_DELETED_NODE
public BBTrieSet(int size) {
mem = new long[size];
freeLists = new long[FREE_LIST_SIZE];
freeIdx = HEADER_SIZE;
root = KNOWN_EMPTY_NODE;
count = 0;
}
private long allocate(int size) {
long free = freeLists[size];
if (free != 0) {
// requested size available in free list, re-link and return head
freeLists[size] = mem[(int) free];
return free;
}
else {
// expansion required?
if (freeIdx + size > mem.length) {
// increase by 25% and assure this is enough
int currSize = mem.length;
int newSize = currSize + Math.max(currSize / 4, size);
mem = Arrays.copyOf(mem, newSize);
}
long idx = freeIdx;
freeIdx += size;
return idx;
}
}
private long allocateInsert(long nodeIdx, int size, int childIdx) {
long newNodeRef = allocate(size + 1);
int a = (int) newNodeRef;
int b = (int) nodeIdx;
// copy with gap for child
for (int j = 0; j < childIdx; j++)
mem[a++] = mem[b++];
a++; // inserted
for (int j = childIdx; j < size; j++)
mem[a++] = mem[b++];
deallocate(nodeIdx, size);
return newNodeRef;
}
private long allocateDelete(long nodeIdx, int size, int childIdx) {
long newNodeRef = allocate(size - 1);
// copy with child removed
int a = (int) newNodeRef;
int b = (int) nodeIdx;
for (int j = 0; j < childIdx; j++)
mem[a++] = mem[b++];
b++; // removed
for (int j = childIdx + 1; j < size; j++)
mem[a++] = mem[b++];
deallocate(nodeIdx, size);
return newNodeRef;
}
private void deallocate(long idx, int size) {
if (idx == KNOWN_EMPTY_NODE)
return; // keep our known empty node
// add to head of free-list
mem[(int) idx] = freeLists[size];
freeLists[size] = idx;
}
private long createLeaf(byte[] key, int off, int len) {
long newNodeRef = allocate(2);
int a = (int) newNodeRef;
mem[a++] = 1L << key[len - 2];
mem[a] = 1L << key[len - 1]; // value
len -= 3;
while (len >= off) {
long newParentNodeRef = allocate(2);
a = (int) newParentNodeRef;
mem[a++] = 1L << key[len--];
mem[a] = newNodeRef;
newNodeRef = newParentNodeRef;
}
return newNodeRef;
}
private long insertChild(long nodeRef, long bitMap, long bitPos, int idx, long value) {
int size = Long.bitCount(bitMap);
long newNodeRef = allocateInsert(nodeRef, size + 1, idx + 1);
mem[(int) newNodeRef] = bitMap | bitPos;
mem[(int) newNodeRef+ 1 + idx] = value;
return newNodeRef;
}
private long removeChild(long nodeRef, long bitMap, long bitPos, int idx) {
int size = Long.bitCount(bitMap);
if (size > 1) {
// node still has other children / leaves
long newNodeRef = allocateDelete(nodeRef, size + 1, idx + 1);
mem[(int) newNodeRef] = bitMap & ~bitPos;
return newNodeRef;
}
else {
// node is now empty, remove it
deallocate(nodeRef, size + 1);
return KNOWN_DELETED_NODE;
}
}
public long size() {
return count;
}
}
Set operations
Contains key
The get method tests, if a key is part of the set. The key is delivered as byte[] where each byte represents one 6-bit bit sequence of the key – so only 6 of the 8 bits per byte are used.
public boolean get(byte[] key, int len) {
if (root == KNOWN_EMPTY_NODE)
return false;
long nodeRef = root;
int off = 0;
for (;;) {
long bitMap = mem[(int) nodeRef];
long bitPos = 1L << key[off++]; // mind the ++
if ((bitMap & bitPos) == 0)
return false; // not found
long value = mem[(int) nodeRef + 1 + Long.bitCount(bitMap & (bitPos - 1))];
if (off == len - 1) {
// at leaf
long bitPosLeaf = 1L << key[off];
return ((value & bitPosLeaf) != 0);
}
else {
// child pointer
nodeRef = value;
}
}
}
Set (add) key
public boolean set(byte[] key, int len) {
long nodeRef = set(root, key, 0, len);
if (nodeRef != KNOWN_EMPTY_NODE) {
// denotes change
count++;
root = nodeRef;
return true;
}
else
return false;
}
private long set(long nodeRef, byte[] key, int off, int len) {
long bitMap = mem[(int) nodeRef];
long bitPos = 1L << key[off++]; // mind the ++
int idx = Long.bitCount(bitMap & (bitPos - 1));
if ((bitMap & bitPos) == 0) {
// child not present yet
long value;
if (off == len - 1)
value = 1L << key[off];
else
value = createLeaf(key, off, len);
return insertChild(nodeRef, bitMap, bitPos, idx, value);
}
else {
// child present
long value = mem[(int) nodeRef + 1 + idx];
if (off == len - 1) {
// at leaf
long bitPosLeaf = 1L << key[off];
if ((value & bitPosLeaf) == 0) {
// update leaf bitMap
mem[(int) nodeRef + 1 + idx] = value | bitPosLeaf;
return nodeRef;
}
else
// key already present
return KNOWN_EMPTY_NODE;
}
else {
// not at leaf, recursion
long childNodeRef = value;
long newChildNodeRef = set(childNodeRef, key, off, len);
if (newChildNodeRef == KNOWN_EMPTY_NODE)
return KNOWN_EMPTY_NODE;
if (newChildNodeRef != childNodeRef)
mem[(int) nodeRef + 1 + idx] = newChildNodeRef;
return nodeRef;
}
}
}
Clear (remove) key
public boolean clear(byte[] key, int len) {
long nodeRef = clear(root, key, 0, len);
if (nodeRef != KNOWN_EMPTY_NODE) {
count--;
if (nodeRef == KNOWN_DELETED_NODE)
root = KNOWN_EMPTY_NODE;
else
root = nodeRef;
return true;
}
else
return false;
}
public long clear(long nodeRef, byte[] key, int off, int len) {
if (root == KNOWN_EMPTY_NODE)
return KNOWN_EMPTY_NODE;
long bitMap = mem[(int) nodeRef];
long bitPos = 1L << key[off++]; // mind the ++
if ((bitMap & bitPos) == 0) {
// child not present, key not found
return KNOWN_EMPTY_NODE;
}
else {
// child present
int idx = Long.bitCount(bitMap & (bitPos - 1));
long value = mem[(int) nodeRef + 1 + idx];
if (off == len - 1) {
// at leaf
long bitPosLeaf = 1L << key[off];
if ((value & bitPosLeaf) == 0)
// key not present
return KNOWN_EMPTY_NODE;
else {
// clear bit in leaf
value = value & ~bitPosLeaf;
if (value != 0) {
// leaf still has some bits set, keep leaf but update
mem[(int) nodeRef + 1 + idx] = value;
return nodeRef;
}
else
return removeChild(nodeRef, bitMap, bitPosLeaf, idx);
}
}
else {
// not at leaf
long childNodeRef = value;
long newChildNodeRef = clear(childNodeRef, key, off, len);
if (newChildNodeRef == KNOWN_EMPTY_NODE)
return KNOWN_EMPTY_NODE;
if (newChildNodeRef == KNOWN_DELETED_NODE)
return removeChild(nodeRef, bitMap, bitPos, idx);
if (newChildNodeRef != childNodeRef)
mem[(int) nodeRef + 1 + idx] = newChildNodeRef;
return nodeRef;
}
}
}
}
Set operators
Set operators for intersection (and), union (or) and difference (minus) are feasible using a flyweight pattern as shown below.
An interface represents physical nodes and "virtual" result nodes of an operator. Instances of this interface are created on demand during a trie traversal. Compound expressions, involving more than one operator, can be expressed directly by combining these operators as an operator can be used as argument (input) for another operator.
Flyweight interface
public interface BBTrieNode {
public long getBitMap();
public long getBitMapLeaf(long bitPos);
public BBTrieNode getChildNode(long bitPos);
}
public static class BBTrieNodeMem implements BBTrieNode {
long nodeRef;
long[] mem;
BBTrieNodeMem child;
public BBTrieNodeMem(long nodeRef, long[] mem) {
this.nodeRef = nodeRef;
this.mem = mem;
}
@Override
public long getBitMap() {
return mem[(int) nodeRef];
}
@Override
public long getBitMapLeaf(long bitPos) {
int idx = Long.bitCount(getBitMap() & (bitPos - 1));
long value = mem[(int) nodeRef + 1 + idx];
return value;
}
@Override
public BBTrieNode getChildNode(long bitPos) {
int idx = Long.bitCount(getBitMap() & (bitPos - 1));
long value = mem[(int) nodeRef + 1 + idx];
return new BBTrieNodeMem(value, mem);
}
}
Intersection (AND)
The intersection operator is very efficient as it automatically performs pruning even over subexpressions. Nonrelevant child nodes don't have to be accessed because the bitmap and a bitwise AND operation allows to determine the result upfront. For example, calculating , the subexpression would not be materialized as intermediate result.
public static class BBTrieAnd implements BBTrieNode {
BBTrieNode nodeA;
BBTrieNode nodeB;
long bitMapA;
long bitMapB;
public BBTrieAnd(BBTrieNode nodeA, BBTrieNode nodeB) {
this.nodeA = nodeA;
this.nodeB = nodeB;
bitMapA = nodeA.getBitMap();
bitMapB = nodeB.getBitMap();
}
public long getBitMap() {
return bitMapA & bitMapB; // this gives a nice optimization (pruning)
}
public long getBitMapLeaf(long bitPos) {
return nodeA.getBitMapLeaf(bitPos) & nodeB.getBitMapLeaf(bitPos);
}
public BBTrieNode getChildNode(long bitPos) {
BBTrieNode childNodeA = nodeA.getChildNode(bitPos);
BBTrieNode childNodeB = nodeB.getChildNode(bitPos);
return new BBTrieAnd(childNodeA, childNodeB);
}
}
Union (OR)
public static class BBTrieOr implements BBTrieNode {
BBTrieNode nodeA;
BBTrieNode nodeB;
long bitMapA;
long bitMapB;
public BBTrieOr(BBTrieNode nodeA, BBTrieNode nodeB) {
this.nodeA = nodeA;
this.nodeB = nodeB;
bitMapA = nodeA.getBitMap();
bitMapB = nodeB.getBitMap();
}
public long getBitMap() {
return bitMapA | bitMapB;
}
public long getBitMapLeaf(long bitPos) {
return nodeA.getBitMapLeaf(bitPos) | nodeB.getBitMapLeaf(bitPos);
}
public BBTrieNode getChildNode(long bitPos) {
if ((bitMapA & bitPos) != 0) {
BBTrieNode childNodeA = nodeA.getChildNode(bitPos);
if ((bitMapB & bitPos) != 0) {
BBTrieNode childNodeB = nodeB.getChildNode(bitPos);
return new BBTrieOr(childNodeA, childNodeB);
}
else
return childNodeA; // optimization, no more or-node required
}
else {
BBTrieNode childNodeB = nodeB.getChildNode(bitPos);
return childNodeB; // optimization, no more or-node required
}
}
}
Difference (MINUS)
public static class BBTrieMinus implements BBTrieNode {
BBTrieNode nodeA;
BBTrieNode nodeB;
long bitMapA;
long bitMapB;
public BBTrieMinus(BBTrieNode nodeA, BBTrieNode nodeB) {
this.nodeA = nodeA;
this.nodeB = nodeB;
bitMapA = nodeA.getBitMap();
bitMapB = nodeB.getBitMap();
}
public long getBitMap() {
return bitMapA; // bitMapB not useful here
}
public long getBitMapLeaf(long bitPos) {
long childBitMapA = nodeA.getBitMapLeaf(bitPos);
if ((bitMapB & bitPos) == 0)
return childBitMapA;
long childBitMapB = nodeB.getBitMapLeaf(bitPos);
return childBitMapA & ~childBitMapB;
}
public BBTrieNode getChildNode(long bitPos) {
BBTrieNode childNodeA = nodeA.getChildNode(bitPos);
if ((bitMapB & bitPos) == 0)
return childNodeA; // optimization, no more minus-node required
BBTrieNode childNodeB = nodeB.getChildNode(bitPos);
return new BBTrieMinus(childNodeA, childNodeB);
}
}
Ranges
Using the virtual node approach, range queries can be accomplished by intersecting a range generating virtual trie (see below) with another operator. So to determine which numbers of a set, say , lay in certain range, say [10..50], instead of iterating through the set and checking each entry, this is performed by evaluating .
public static class BBTrieIntRange implements BBTrieNode {
private long bitMap;
private int a, b;
private int x, y;
private int level;
public BBTrieIntRange(int a, int b) {
this(a, b, 5);
}
private BBTrieIntRange (int a, int b, int level) {
this.a = a;
this.b = b;
this.level = level;
x = (int) (a >>> (level * 6)) & 0x3F;
y = (int) (b >>> (level * 6)) & 0x3F;
// bit hack for: for (int i = x; i <= y; i++) bitSet |= (1L << i);
bitMap = 1L << y;
bitMap |= bitMap - 1;
bitMap &= ~((1L << x) - 1);
}
public long getBitMap() {
return bitMap;
}
public long getBitMapLeaf(long bitPos) {
// simple solution for readability (not that efficient as for each call a child is created again)
return getChildNode(bitPos).getBitMap();
}
public BBTrieIntRange getChildNode(long bitPos) {
int bitNum = Long.numberOfTrailingZeros(bitPos);
if (x == y)
return new BBTrieIntRange(a, b, level - 1);
else if (bitNum == x)
return new BBTrieIntRange(a, ~0x0, level - 1);
else if (bitNum == y)
return new BBTrieIntRange(0, b, level - 1);
else
return new BBTrieIntRange(0, ~0x0, level - 1);
}
}
Usage example
The example shows the usage with 32-bit integers as keys.
public class BBTrieSetSample {
public interface Visitor {
public void visit(byte[] key, int keyLen);
}
public static void visit(BBTrieNode node, Visitor visitor, byte[] key, int off, int len) {
long bitMap = node.getBitMap();
if (bitMap == 0)
return;
long bits = bitMap;
while (bits != 0) {
long bitPos = bits & -bits; bits ^= bitPos; // get rightmost bit and clear it
int bitNum = Long.numberOfTrailingZeros(bitPos);
key[off] = (byte) bitNum;
if (off == len - 2) {
long value = node.getBitMapLeaf(bitPos);
long bits2 = value;
while (bits2 != 0) {
long bitPos2 = bits2 & -bits2; bits2 ^= bitPos2;
int bitNum2 = Long.numberOfTrailingZeros(bitPos2);
key[off+1] = (byte) bitNum2;
visitor.visit(key, off + 2);
}
}
else {
BBTrieNode childNode = node.getChildNode(bitPos);
visit(childNode, visitor, key, off + 1, len);
}
}
}
public static int set6Int(byte[] b, int value) {
int pos = 0;
b[pos ] = (byte) ((value >>> 30) & 0x3F);
b[pos + 1] = (byte) ((value >>> 24) & 0x3F);
b[pos + 2] = (byte) ((value >>> 18) & 0x3F);
b[pos + 3] = (byte) ((value >>> 12) & 0x3F);
b[pos + 4] = (byte) ((value >>> 6) & 0x3F);
b[pos + 5] = (byte) (value & 0x3F);
return 6;
}
public static int get6Int(byte[] b) {
int pos = 0;
return
((b[pos ] & 0x3F) << 30) |
((b[pos + 1] & 0x3F) << 24) |
((b[pos + 2] & 0x3F) << 18) |
((b[pos + 3] & 0x3F) << 12) |
((b[pos + 4] & 0x3F) << 6) |
(b[pos + 5] & 0x3F);
}
public static void main(String[] args) {
BBTrieSet trie1 = new BBTrieSet(100);
BBTrieSet trie2 = new BBTrieSet(100);
byte[] key = new byte[64];
int len;
final int KEY_LEN_INT = set6Int(key, 1); // 6
int[] test = new int[] { 10, 20, 30, 40, 50, 30, 60, 61, 62, 63 };
for (int i = 0; i < test.length; i++) {
len = set6Int(key, test[i]);
boolean change = trie1.set(key, len);
System.out.println("set: " + test[i] + ", " + change);
}
System.out.println("trie1 size: " + trie1.size());
BBTrieSetOps.visit(new BBTrieNodeMem(trie1.root, trie1.mem), new BBTrieSetOps.Visitor() {
@Override
public void visit(byte[] key, int keyLen) {
System.out.println("Visitor: "+ get6Int(key) + ", " + keyLen);
}
}, key, 0, KEY_LEN_INT);
test = new int[] { 10, 25, 30, 40, 45, 50, 55, 60 };
for (int i = 0; i < test.length; i++) {
len = set6Int(key, test[i]);
boolean contained = trie1.get(key, len);
System.out.println("contained: " + test[i] + ", " + contained);
}
test = new int[] { 10, 20, 30, 40, 45, 50, 55, 60, 61, 62, 63 };
for (int i = 0; i < test.length; i++) {
len = set6Int(key, test[i]);
boolean change = trie1.clear(key, len);
System.out.println("cleared: " + test[i] + ", " + change);
BBTrieSetOps.visit(new BBTrieNodeMem(trie1.root, trie1.mem), new BBTrieSetOps.Visitor() {
@Override
public void visit(byte[] key, int keyLen) {
System.out.print(get6Int(key) + " ");
}
}, key, 0, KEY_LEN_INT);
System.out.println();
}
System.out.println("trie1 size: " + trie1.size());
for (int i = 0; i <= 50; i++) {
len = set6Int(key, i);
trie1.set(key, len);
System.out.println("set: " + i);
}
System.out.println("trie1 size: " + trie1.size());
for (int i = 25; i <= 75; i++) {
len = set6Int(key, i);
trie2.set(key, len);
System.out.println("set: " + i);
}
System.out.println("trie2 size: " + trie2.size());
// AND example
BBTrieNode result = new BBTrieAnd(
new BBTrieNodeMem(trie1.root, trie1.mem),
new BBTrieNodeMem(trie2.root, trie2.mem));
BBTrieSetOps.visit(result, new BBTrieSetOps.Visitor() {
@Override
public void visit(byte[] key, int keyLen) {
System.out.println("Visitor AND result: " + get6Int(key));
}
}, key, 0, KEY_LEN_INT);
}
}
References
- ↑ Phil Bagwell (2000). Fast And Space Efficient Trie Searches (PDF) (Report). Infoscience Department, École Polytechnique Fédérale de Lausanne.
- ↑ Warren Jr., Henry S. (2013). Hacker's Delight (2 ed.). Addison Wesley - Pearson Education, Inc. ISBN 978-0-321-84268-8.
- ↑ EP patent 3376407, Walter Bauer, "Efficient use of trie data structure in databases", published 2018-09-19, issued 2020-09-16, assigned to censhare AG