A Reuleaux triangle, a curve of constant width whose area is minimum among all convex sets with the same width

In plane geometry the Blaschke–Lebesgue theorem states that the Reuleaux triangle has the least area of all curves of given constant width.^[1] In the form that every curve of a given width has area at least as large as the Reuleaux triangle, it is also known as the Blaschke–Lebesgue inequality.^[2] It is named after Wilhelm Blaschke and Henri Lebesgue, who published it separately in the early 20th century.

Statement

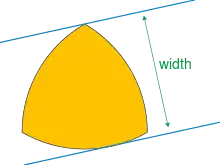
The width of a convex set ${\displaystyle K}$ in the Euclidean plane is defined as the minimum distance between any two parallel lines that enclose it. The two minimum-distance lines are both necessarily tangent lines to ${\displaystyle K}$, on opposite sides. A curve of constant width is the boundary of a convex set with the property that, for every direction of parallel lines, the two tangent lines with that direction that are tangent to opposite sides of the curve are at a distance equal to the width. These curves include both the circle and the Reuleaux triangle, a curved triangle formed from arcs of three equal-radius circles each centered at a crossing point of the other two circles. The area enclosed by a Reuleaux triangle with width ${\displaystyle w}$ is

${\displaystyle {\frac {1}{2}}(\pi -{\sqrt {3}})w^{2}\approx 0.70477w^{2}.}$

The Blaschke–Lebesgue theorem states that this is the unique minimum possible area of a curve of constant width, and the Blaschke–Lebesgue inequality states that every convex set of width ${\displaystyle w}$ has area at least this large, with equality only when the set is bounded by a Reuleaux triangle.^[1]

History

The Blaschke–Lebesgue theorem was published independently in 1914 by Henri Lebesgue^[3] and in 1915 by Wilhelm Blaschke.^[4] Since their work, several other proofs have been published.^{[5][6][7][8][9][10]}

In other planes

The same theorem is also true in the hyperbolic plane.^[11] For any convex distance function on the plane (a distance defined as the norm of the vector difference of points, for any norm), an analogous theorem holds true, according to which the minimum-area curve of constant width is an intersection of three metric disks, each centered on a boundary point of the other two.^[12][13]

Application

The Blaschke–Lebesgue theorem has been used to provide an efficient strategy for generalizations of the game of Battleship, in which one player has a ship formed by intersecting the integer grid with a convex set and the other player, after having found one point on this ship, is aiming to determine its location using the fewest possible missed shots. For a ship with ${\displaystyle n}$ grid points, it is possible to bound the number of missed shots by ${\displaystyle O(\log \log n)}$.^[14]

Related problems

By the isoperimetric inequality, the curve of constant width in the Euclidean plane with the largest area is a circle.^[1] The perimeter of a curve of constant width ${\displaystyle w}$ is ${\displaystyle \pi w}$, regardless of its shape; this is Barbier's theorem.^[15]

It is unknown which surfaces of constant width in three-dimensional space have the minimum volume. Bonnesen and Fenchel conjectured in 1934 that the minimizers are the two Meissner bodies obtained by rounding some of the edges of a Reuleaux tetrahedron,^[16] but this remains unproven.^[17]

References