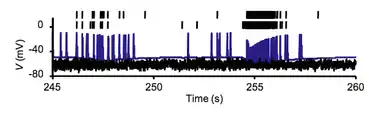
Bursting, or burst firing, is an extremely diverse[1] general phenomenon of the activation patterns of neurons in the central nervous system[2][3] and spinal cord[4] where periods of rapid action potential spiking are followed by quiescent periods much longer than typical inter-spike intervals. Bursting is thought to be important in the operation of robust central pattern generators,[5][6][7] the transmission of neural codes,[8][9] and some neuropathologies such as epilepsy.[10] The study of bursting both directly and in how it takes part in other neural phenomena has been very popular since the beginnings of cellular neuroscience and is closely tied to the fields of neural synchronization, neural coding, plasticity, and attention.
Observed bursts are named by the number of discrete action potentials they are composed of: a doublet is a two-spike burst, a triplet three and a quadruplet four. Neurons that are intrinsically prone to bursting behavior are referred to as bursters and this tendency to burst may be a product of the environment or the phenotype of the cell.
Physiological context
Overview
Neurons typically operate by firing single action potential spikes in relative isolation as discrete input postsynaptic potentials combine and drive the membrane potential across the threshold. Bursting can instead occur for many reasons, but neurons can be generally grouped as exhibiting input-driven or intrinsic bursting. Most cells will exhibit bursting if they are driven by a constant, subthreshold input[11] and particular cells which are genotypically prone to bursting (called bursters) have complex feedback systems which will produce bursting patterns with less dependence on input and sometimes even in isolation.[3][11]
In each case, the physiological system is often thought as being the action of two linked subsystems. The fast subsystem is responsible for each spike the neuron produces. The slow subsystem modulates the shape and intensity of these spikes before eventually triggering quiescence.
Input-driven bursting often encodes the intensity of input into the bursting frequency[11] where a neuron then acts as an integrator. Intrinsic bursting is a more specialized phenomenon and is believed to play a much more diverse role in neural computation.
Fast subsystem
Slow subsystem
Bursts differ from tonic firing, typically associated with Poisson distributed spike times for a given average firing rate, in that bursting involves a physiological "slow subsystem" that eventually depletes as the bursting continues and then must be replenished before the cell can burst again (compare refractory period).[11] During the bursting event, this slow subsystem modulates the timing and intensity of the emitted spikes and is thought to be important in the computational aspects of the resulting burst pattern. There are many discovered mechanisms of slow subsystems including voltage-[6][12][13] and Ca2+-gated[14] currents and spiking interplay between dendrites and the cell body.[15]
The slow subsystem also is connected to endogenous bursting patterns in neurons, where the pattern can be maintained completely by internal mechanism without any synaptic input. This process also relies on calcium channels, which depolarize the neuron by allowing an influx of calcium ions. So long as internal calcium ion concentrations remain at an elevated level, the neuron will continue to undergo periods of rapid spiking. However, elevated calcium ion levels also trigger a second messenger cascade within the cell which lower calcium influx and promote calcium efflux and buffering. As calcium concentrations decline, the period of rapid bursting ceases, and the phase of quiescence begins. When calcium levels are low, the original calcium channels will reopen, restarting the process and creating a bursting pattern.[16]
Statistical detection
In isolation or in mathematical models bursting can be recognized since the environment and state of the neuron can be carefully observed and modulated. When observing neurons in the wild, however, bursting may be difficult to distinguish from normal firing patterns. In order to recognize bursting patterns in these contexts statistical methods are used to determine threshold parameters.
Bursting is characterized by a coefficient of variation (CV) of the interspike intervals (ISI) that is larger than one, or a Fano factor of the spike count that is larger than one, because bursting leads to spike patterns that are more irregular than a Poisson process (which has a CV and Fano factor equal to unity). Alternatively, the serial correlation coefficient of the ISI sequence is positive for bursting patterns, because in this case short ISIs tend to be followed by more short ISIs (at least if the bursts consist of more than two spikes).
Mathematical models
Neuron behavior is often modeled as single-compartment, non-linear dynamical systems, where the neuron states represent physiological quantities such as membrane voltage, current flow, and the concentrations of various ions intra- and extracellularly. These models most generally take the singularly perturbed form
- fast subsystem:
- slow subsystem:
where and are both Hodgkin–Huxley style relations, is a vector representing the cell parameters relevant to the fast subsystem, is a vector representing the parameters of the slow modulation subsystem, and is the ratio of the time scales between the fast and slow subsystems.[11]
Models of neuron dynamics generally exhibit a number of stable and unstable attractors in phase space which represent resting states. When the system is sufficiently perturbed by input stimuli it may follow a complex return path back to the stable attractor representing an action potential. In bursting neurons, these dynamic spaces bifurcate between quiescent and bursting modes according to the dynamics of the slow system. These two bifurcations may take many forms and the choice of bifurcation both from quiescent to bursting and bursting to quiescent can affect the behavioral aspects of the burster.
The complete classification of quiescent-to-bursting and bursting-to-quiescent bifurcations leads to 16 common forms and 120 possible forms if the dimensionality of the fast subsystem is not constrained.[11] Of the most common 16, a few are well studied.
| saddle node on an invariant circle | saddle homoclinic orbit | supercritical Andronov-Hopf | fold limit cycle | |
|---|---|---|---|---|
| saddle node (fold) | fold/ circle | fold/ homoclinic | fold/ Hopf | fold/ fold cycle |
| saddle node on an invariant circle | circle/ circle | circle/ homoclinic | circle/ Hopf | circle/ fold cycle |
| supercritical Andronov-Hopf | Hopf/ circle | Hopf/ homoclinic | Hopf/ Hopf | Hopf/ fold cycle |
| subcritical Andronov-Hopf | subHopf/ circle | subHopf/ homoclinic | subHopf/ Hopf | subHopf/ fold cycle |
Square-wave burster
The fold/homoclinic, also called square-wave, burster is so named because the shape of the voltage trace during a burst looks similar to a square wave due to fast transitions between the resting state attractor and the spiking limit cycle.[11]
Purposes
Bursting is a very general phenomenon and is observed in many contexts in many neural systems. For this reason it is difficult to find a specific meaning or purpose for bursting and instead it plays many roles. In any given circuit observed bursts may play a part in any or all of the following mechanisms and may have a still more sophisticated impact on the network.
Synaptic plasticity
Synaptic strengths between neurons follow changes that depend on spike timing and bursting. For excitatory synapses of the cortex, pairing an action potential in the pre-synaptic neuron with a burst in the post-synaptic neuron leads to long-term potentiation of the synaptic strength, while pairing an action potential in the pre-synaptic neuron with a single spike in the post-synaptic neuron leads to long-term depression of the synaptic strength.[17] Such dependence of synaptic plasticity on the spike timing patterns is referred to as burst-dependent plasticity. Burst-dependent plasticity is observed with variations in multiple areas of the brain. [18]
Multiplexing and routing
Some neurons, sometimes called resonators, exhibit sensitivity for specific input frequencies and fire either more quickly or exclusively when stimulated at that frequency. Intrinsically bursting neurons can use this band-pass filtering effect in order to encode for specific destination neurons and multiplex signals along a single axon.[11] More generally, due to short-term synaptic depression and facilitation specific synapses can be resonant for certain frequencies and thus become viable specific targets for bursting cells.[19] When combined with burst-dependent long-term plasticity, such multiplexing can allow neurons to coordinate synaptic plasticity across hierarchical networks.[17][20]
Synchronization
Burst synchronization refers to the alignment of bursting and quiescent periods in interconnected neurons. In general, if a network of bursting neurons is linked it will eventually synchronize for most types of bursting.[11][21][22] Synchronization can also appear in circuits containing no intrinsically bursting neurons, however its appearance and stability can often be improved by including intrinsically bursting cells in the network.[7] Since synchronization is related to plasticity and memory via Hebbian plasticity and long-term potentiation the interplay with plasticity and intrinsic bursting is very important.
Information content and channel robustness
Due to the all-or-nothing nature of action potentials, single spikes can only encode information in their interspike intervals (ISI). This is an inherently low fidelity method of transferring information as it depends on very accurate timing and is sensitive to noisy loss of signal: if just a single spike is mistimed or not properly received at the synapse it leads to a possibly unrecoverable loss in coding. Since intrinsic bursts are thought to be derived by a computational mechanism in the slow subsystem, each can represent a much larger amount of information in the specific shape of a single burst leading to far more robust transmission. Physiological models show that for a given input the interspike and interburst timings are much more variable than the timing of the burst shape itself[9] which also implies that timing between events is a less robust way to encode information.
The expanded alphabet for communication enabled by considering burst patterns as discrete signals allows for a greater channel capacity in neuronal communications and provides a popular connection between neural coding and information theory.
Example bursting neuron circuits
Hippocampus
The subiculum, a component of the hippocampal formation, is thought to perform relaying of signals originating in the hippocampus to many other parts of the brain.[23] In order to perform this function, it uses intrinsically bursting neurons to convert promising single stimuli into longer lasting burst patterns as a way to better focus attention on new stimuli and activate important processing circuits.[2][24] Once these circuits have been activated, the subicular signal reverts to a single spiking mode.[25]
pre-Bötzinger complex
The pre-Bötzinger complex (preBötC) is located in ventrolateral medulla and is proposed to generate the rhythm underlying inspiratory efforts in mammals. Since the frequency that the lungs need to operate at can vary according to metabolic demand, preBötC activity is modulated over a wide range of frequencies and is able to entrain the respiratory system to meet metabolic demand. While pacemaker neurons do not necessarily require intrinsically bursting neurons[21] the preBötC contains a heterogeneous population of both regular spiking and intrinsically bursting neurons. Intrinsically bursting neurons are thought to make the preBötC oscillations more robust to changing frequencies and the regularity of inspiratory efforts.[7]
Cerebellar cortex
Cerebellar Purkinje neurons have been proposed to have two distinct bursting modes: dendritically driven, by dendritic Ca2+
spikes,[26] and somatically driven, wherein the persistent Na+
current is the burst initiator and the SK K+
current is the burst terminator.[27] Purkinje neurons may utilise these bursting forms in information coding to the deep cerebellar nuclei.
See also
References
- ↑ Wagenaar, Daniel; Jerome Pine; Steve M. Potter (2006-02-07). "An extremely rich repertoire of bursting patterns during the development of cortical cultures". BMC Neuroscience. 7: 11. doi:10.1186/1471-2202-7-11. PMC 1420316. PMID 16464257.
- 1 2 Cooper, D (2002). "The significance of action potential bursting in the brain reward circuit". Neurochemistry International. 41 (5): 333–340. doi:10.1016/S0197-0186(02)00068-2. PMID 12176075. S2CID 22492183.
- 1 2 Jeffreys, JGR; HL Hass (1982-12-02). "Synchronized bursting of CA1 hippocampal pyramidal cells in the absence of synaptic transmission". Letters to Nature. 300 (5891): 448–450. Bibcode:1982Natur.300..448J. doi:10.1038/300448a0. PMID 6292731. S2CID 2767619.
- ↑ Smith, JC; HH Ellenberger; K Ballanyi; DW Richter; JL Feldman (November 1991). "Pre-Botzinger complex: a brainstem region that may generate respiratory rhythm in mammals". Science. 254 (5032): 726–729. Bibcode:1991Sci...254..726S. doi:10.1126/science.1683005. PMC 3209964. PMID 1683005.
- ↑ Marder, E (2000). "Motor pattern generation". Current Opinion in Neurobiology. 10 (6): 691–698. doi:10.1016/S0959-4388(00)00157-4. PMID 11240277. S2CID 19743807.
- 1 2 Butera, Robert; John Rinzel; Jeffrey Smith (1999). "Models of Respiratory Rhythm Generation in the Pre-Botzinger Complex. I. Bursting Pacemaker Neurons". Journal of Neurophysiology. 82 (1): 382–97. doi:10.1152/jn.1999.82.1.382. PMID 10400966. S2CID 396589.
- 1 2 3 Butera, Robert; John Rinzel; Jeffrey Smith (January 1999). "Models of respiratory rhythm generation in the pre-Botzinger complex. II. Populations of Coupled Pacemaker Neurons". Journal of Neurophysiology. 82 (1): 1349–56. doi:10.1152/jn.1999.82.1.398. PMID 10400967. S2CID 17905991.
- ↑ Kepecs, A; X Wang; J Lisman (2002). "Bursting Neurons Signal Input Slope". Journal of Neuroscience. 22 (20): 9053–62. doi:10.1523/JNEUROSCI.22-20-09053.2002. PMC 6757694. PMID 12388612.
- 1 2 Kepecs, A; J Lisman (2003-01-01). "Information encoding and computation with spikes and bursts". Network: Computation in Neural Systems. 14 (1): 103–118. doi:10.1080/net.14.1.103.118. PMID 12613553. S2CID 1553645.
- ↑ Prince, David A (March 1978). "Neurophysiology of Epilepsy". Annual Review of Neuroscience. 1: 395–415. doi:10.1146/annurev.ne.01.030178.002143. PMID 386906.
- 1 2 3 4 5 6 7 8 9 Izhikevich, Eugene (2000-01-01). "Neural excitability, spiking and bursting" (PDF). International Journal of Bifurcation and Chaos. 10 (6): 1171–1266. Bibcode:2000IJBC...10.1171I. CiteSeerX 10.1.1.421.2424. doi:10.1142/S0218127400000840. Retrieved 2009-11-30.
- ↑ Wang, X (1999). "Fast burst firing and short-term synaptic plasticity: a model of neocortical chattering neurons". Neuroscience. 89 (2): 347–362. doi:10.1016/S0306-4522(98)00315-7. PMID 10077318. S2CID 24600653.
- ↑ Huguenard, John; D McCormick (1992). "Simulation of the currents involved in rhythmic oscillations in thalamic relay neurons". Journal of Neurophysiology. 68 (4): 1373–83. CiteSeerX 10.1.1.320.1988. doi:10.1152/jn.1992.68.4.1373. PMID 1279135.
- ↑ Kloppenburg, Peter; Warren Zipfel; Watt Webb; Ronald Harris-Warrick (2000-04-01). "Highly Localized Ca2+ Accumulation Revealed by Multiphoton Microscopy in an Identified Motoneuron and Its Modulation by Dopamine". Journal of Neuroscience. 20 (7): 2523–33. doi:10.1523/JNEUROSCI.20-07-02523.2000. PMC 6772235. PMID 10729332.
- ↑ Doiron, Brent; Maurice J Chacron; Leonard Maler; André Longtin; Joseph Bastian (2003-01-30). "Inhibitory feedback required for network oscillatory responses to communication but not prey stimuli". Nature. 421 (6922): 539–543. Bibcode:2003Natur.421..539D. doi:10.1038/nature01360. PMID 12556894. S2CID 4407550.
- ↑ Bryne, John. "Feedback/recurrent inhibition in nanocircuits". Neuroscience Online. University of Texas Health Center. Archived from the original on 2015-04-26. Retrieved 2013-07-27.
- 1 2 Payeur, Alexandre; J Guergiuev; F Zenke; B A Richards; R Naud (2021). "Burst-dependent synaptic plasticity can coordinate learning in hierarchical circuits". Nature Neuroscience. 24 (6): 1010–1019. doi:10.1038/s41593-021-00857-x. ISSN 1097-6256. PMID 33986551. S2CID 214793776.
- ↑ Friedenberger, Zachary; E Harkin; K Toth; R Naud (2023). "Silences, spikes and bursts: Three-part knot of the neural code". Journal of Physiology. 601: 5165–5193. arXiv:2302.07206. doi:10.1113/JP281510.
- ↑ Izhikevich, Eugene; N Desai; E Walcott (2003). "Bursts as a unit of neural information: selective communication via resonance". Trends in Neurosciences. 26 (3): 161–7. doi:10.1016/S0166-2236(03)00034-1. PMID 12591219. S2CID 698477.
- ↑ Naud, Richard; H Sprekeler (2018). "Sparse bursts optimize information transmission in a multiplexed neural code". PNAS. 115 (27): E6329–E6338. Bibcode:2018PNAS..115E6329N. doi:10.1073/pnas.1720995115. PMC 6142200. PMID 29934400.
- 1 2 Rulkov, NF (March 2001). "Regularization of synchronized chaotic bursts". Physical Review Letters. 86 (1): 183–6. arXiv:nlin/0011028. Bibcode:2001PhRvL..86..183R. doi:10.1103/PhysRevLett.86.183. PMID 11136124. S2CID 7016788.
- ↑ Belykh, I; E de Lange; M Hasler (2005). "Synchronization of bursting neurons: what matters in the network topology". Physical Review Letters. 94 (18): 2181. Bibcode:2005PhRvL..94r8101B. doi:10.1103/PhysRevLett.94.188101. PMID 15904412.
- ↑ Swanson, LW; WM Cowan (1977-03-01). "An autoradiographic study of the organization of the efferent connections of the hippocampal formation in the rat". Journal of Computational Neurology. 172 (1): 49–84. doi:10.1002/cne.901720104. PMID 65364. S2CID 40742028.
- ↑ Swadlow, H; A Gusev; T Bezdudnaya (2002-01-01). "Activation of a cortical column by a thalamocortical impulse". Journal of Neuroscience. 22 (17): 7766–7773. doi:10.1523/JNEUROSCI.22-17-07766.2002. PMC 6757983. PMID 12196600.
- ↑ Cooper, DC; S Chung; N Spruston (June 2005). "Output-mode transitions are controlled by prolonged inactivation of sodium channels in pyramidal neurons of subiculum". PLOS Biology. 3 (6): 1123. doi:10.1371/journal.pbio.0030175. PMC 1088280. PMID 15857153.
- ↑ Forrest MD, Wall MJ, Press DA, Feng J (December 2012). "The Sodium-Potassium Pump Controls the Intrinsic Firing of the Cerebellar Purkinje Neuron". PLOS ONE. 7 (12): e51169. Bibcode:2012PLoSO...751169F. doi:10.1371/journal.pone.0051169. PMC 3527461. PMID 23284664.
- ↑ Forrest MD (August 2013). "Mathematical Model of Bursting in Dissociated Purkinje Neurons". PLOS ONE. 8 (8): e68765. Bibcode:2013PLoSO...868765F. doi:10.1371/journal.pone.0068765. PMC 3742666. PMID 23967054.
Rinzel J. (1986) A formal Classification of Bursting Mechanisms in Excitable Systems. Proceedings of the International Congress of Mathematicians. Berkeley, California, USA
External links
Izhikevich E. M. (2006) Bursting. Scholarpedia, 1(3):1300