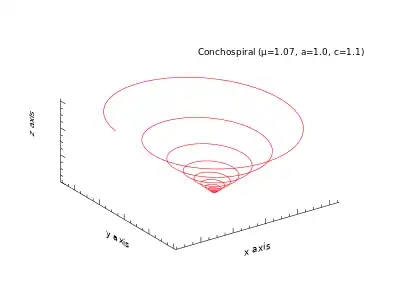
An example
An example

In mathematics, a conchospiral a specific type of space spiral on the surface of a cone (a conical spiral), whose floor projection is a logarithmic spiral. Conchospirals are used in biology for modelling snail shells, and flight paths of insects [1][2] and in electrical engineering for the construction of antennas.[3][4]

Parameterization

In cylindrical coordinates, the conchospiral is described by the parametric equations:

The projection of a conchospiral on the plane is a logarithmic spiral. The parameter controls the opening angle of the projected spiral, while the parameter controls the slope of the cone on which the curve lies.

History

The name "conchospiral" was given to these curves by 19th-century German mineralogist Georg Amadeus Carl Friedrich Naumann, in his study of the shapes of sea shells.[5]

Applications

The conchospiral has been used in the design for radio antennas. In this application, it has the advantage of producing a radio beam in a single direction, towards the apex of the cone.[6][7]

References

  1. ↑ New Scientist
  2. ↑ Conchospirals in the Flight of Insects
  3. ↑ John D. Dyson: The Equiangular Spiral Antenna. In: IRE Transactions on Antennas and Propagation. Vol. 7, 1959, pp. 181–187.
  4. ↑ T. A. Kozlovskaya: The Concho-Spiral on the Cone. Vestn. Novosib. Gos. Univ., Ser. Mat. Mekh. Inform., 11:2 (2011), pp. 65–76.
  5. ↑ Blake, John Frederick (1882), A Monograph of the British Fossil Cephalopoda, Part 1, J. Van Voorst, p. 23
  6. ↑ Burberry, R. A. (1992), "8.2.4 Conical spiral", VHF and UHF Antennas, Institution of Electrical Engineers Electromagnetic Waves Series, vol. 35, IET, p. 142, ISBN 9780863412691
  7. ↑ Balanis, Constantine A. (2015), "11.3.2 Conical spiral", Antenna Theory: Analysis and Design, John Wiley & Sons, p. 598, ISBN 9781119178989
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.