Conservative formula investing is an investment technique that uses the principles of low-volatility investing and is enhanced with momentum and net payout yield signals.

Methodology

The Conservative formula based on 3 investment criteria: volatility, momentum and net payout yield.

1. From the 1,000 largest stocks the 500 with the lowest historical 36-month stock return volatility are selected
2. Using this subset, each stock is then ranked on its 12-1 month price momentum and net payout yield
3. Thereafter, the momentum and net payout yield rankings (1 to 500) are averaged and the best 100 stocks are equally weighted in a final portfolio that is rebalanced on a quarterly basis

For more background, the Conservative Formula is discussed and replicated in an August 2022 Bloomberg webinar.^[1] It is also included as a stock screener on Validea and ValueSignals.^[2][3] In addition, it can be replicated through the use of the code that is shared on Reddit and Medium.^[4][5]

Background

Similar to Joel Greenblatt's Magic Formula of Joel Greenblatt, the Conservative Formula is used as a stock screener that aims to beat the market. It is designed to achieve higher risk-adjusted returns in a systematic manner, by giving investors exposure to multiple investment factors using easily obtainable data. The formula is outlined in a book 'High Returns from Low Risk' which is written by Pim van Vliet and Jan de Koning.^[6] It was published in 2016 and translated into Chinese, German, French, Spanish and Dutch.^{[7][8][9][10][11]} It has also been empirically tested in an academic paper by David Blitz and Pim van Vliet which is publicly available on SSRN.^[12][13]

In 2019 and 2022 the Conservative Formula was applied to the Chinese A-share and Indian stock markets by independent researchers.^[14][15] It has also been discussed on multiple platforms including Alpha Architect, GuruFocus, La Vanguardia and ETF.com as well as reviewed on JD.com.^{[16][17][18][19][7]}

US results

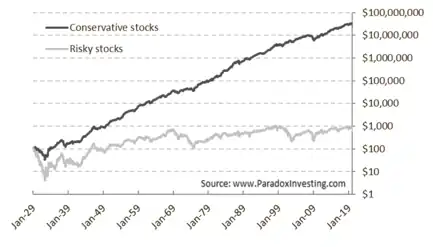
Based on a universe of US stocks, the Conservative Formula has produced an annualized return of 15.1% over the period January 1929 to December 2016, significantly outperforming the US market index by 5.8% per year. Moreover, this return has been achieved with lower volatility, resulting in a Sharpe ratio of 0.94 for the full sample period. The formula also delivered positive returns in each decade in this market.

The historical return series dating back to 1929 are publicly available and updated every year.^[20] The figure shows the cumulative US dollar performance of Conservative versus Speculative (i.e., high volatility stocks with weak momentum and low net payout yields) stocks, including recent out-of-sample results.

International results

The Conservative Formula has also been applied to international markets, where it generated annualized returns of 15.4% in Europe versus 7.4% for the market, and annualized gains of 9.6% in Japan compared to 0.3% for the market, both for the period January 1986 to December 2016. In emerging markets, the formula has resulted in annualized performance of 19.3% against 6.3% for the market, over the period January 1993 to December 2016. In each case, the higher returns were achieved with lower volatility.^[12]

For the Chinese A-share market, the formula delivered annualized returns of 10.9% versus 1.4% for the CSI-300 Index for the period August 2008 to August 2018, with lower volatility.^[14] In India, it significantly outperformed the S&P BSE 100 Index by 12.6% per annum over the period September 2006 to June 2022, also with lower volatility.^[15]

Criticism of Conservative Formula

1. During the first quarter of 2020, low volatility stocks offered little risk reduction during the Covid-induced sell-off, while they also lagged during the subsequent sharp market rebound. As a result, some investors lost faith in the low-volatility approach.^[21][22]
2. The quoted returns are gross of transaction costs. Net returns would typically be between 0.3% and 0.8% lower, based on the estimated range for annual transaction costs in international developed markets.^[13]
3. Due to hindsight bias and p-hacking the power of the formula may be overestimated.

While these critical points are relevant, out-of-sample tests can help falsify or verify the results of the original study. To this end, the Conservative Formula has been applied to other markets – such as the Chinese-A share and Indian equity markets – and exhibited strong results. For the US, the pre-sample evidence also reflects robust results for the period from January 1866 to December 1928.^[23] Moreover, the post-publication results are positive despite the underperformance experienced in 2020. But since this accounts for a relatively short period, no strong and final conclusions can be drawn.

See also

• Low-volatility investing
• Magic formula investing
• Piotroski F-score
• Momentum investing

References