In crystallography, a disclination is a line defect in which rotational symmetry is violated.[1] In analogy with dislocations in crystals, the term, disinclination, for liquid crystals first used by Frederick Charles Frank and since then has been modified to its current usage, disclination.[2] It is a defect in the orientation of director whereas a dislocation is a defect in positional order.[3]

Example in two dimensions

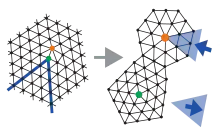
Formation of two disclinations (right) out of a dislocation (left) on an otherwise hexagonal background

In 2D, disclinations and dislocations are point defects instead of line defects as in 3D. They are topological defects and play a central role in melting of 2D crystals within the KTHNY theory, based on two Kosterlitz–Thouless transitions.

Equally sized discs (spheres, particles, atoms) form a hexagonal crystal as dense packing in two dimensions. In such a crystal, each particle has six nearest neighbors. Local strain and twist (for example induced by thermal motion) can cause configurations where discs (or particles) have a coordination number different of six, typically five or seven. Disclinations are topological defects, therefore (starting from a hexagonal array) they can only be created in pairs. Ignoring surface/border effects, this implies that there are always as many 5-folded as 7-folded disclinations present in a perfectly plane 2D crystal. A "bound" pair of 5-7-folded disclinations is a dislocation. If myriad dislocations are thermally dissociated into isolated disclinations, then the monolayer of particles becomes an isotropic fluid in two dimensions. A 2D crystal is free of disclinations.

To transform a section of a hexagonal array into a 5-folded disclination (colored green in the figure), a triangular wedge of hexagonal elements (blue triangle) has to be removed; to create a 7-folded disclination (orange), an identical wedge must be inserted. The figure illustrates how disclinations destroy orientational order, while dislocations only destroy translational order in the far field (portions of the crystal far from the center of the disclination).

Disclinations are topological defects because they cannot be created locally by an affine transformation without cutting the hexagonal array outwards to infinity (or the border of a finite crystal). The undisturbed hexagonal crystal has a  60° symmetry, but when a wedge is removed to create a 5-folded disclination, the crystal symmetry is stretched to  72° – for a 7-folded disclination, it is compressed to about  51,4°. Thus, disclinations store elastic energy by disturbing the director field.

See also

References

  1. ↑ Murayama, M.; Howe, J. M.; Hidaka, H.; Takaki, S. (2002-03-29). "Atomic-Level Observation of Disclination Dipoles in Mechanically Milled, Nanocrystalline Fe". Science. 295 (5564): 2433–2435. Bibcode:2002Sci...295.2433M. doi:10.1126/science.1067430. PMID 11923534. S2CID 46024551.
  2. ↑ Chandrasekhar, S. (1977) Liquid Crystals, Cambridge University Press, p. 123, ISBN 0-521-21149-2
  3. ↑ Barón, Máximo (2001). "Definitions of basic terms relating to low-molar-mass and polymer liquid crystals (IUPAC Recommendations 2001)". Pure and Applied Chemistry. 73 (5): 845–895. doi:10.1351/pac200173050845. S2CID 95656853.

Further reading

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.