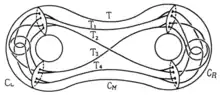
The first stage of the dogbone space construction.

In geometric topology, the dogbone space, constructed by R. H. Bing (1957), is a quotient space of three-dimensional Euclidean space ${\displaystyle \mathbb {R} ^{3}}$ such that all inverse images of points are points or tame arcs, yet it is not homeomorphic to ${\displaystyle \mathbb {R} ^{3}}$. The name "dogbone space" refers to a fanciful resemblance between some of the diagrams of genus 2 surfaces in R. H. Bing's paper and a dog bone. Bing (1959) showed that the product of the dogbone space with ${\displaystyle \mathbb {R} ^{1}}$ is homeomorphic to ${\displaystyle \mathbb {R} ^{4}}$.

Although the dogbone space is not a manifold, it is a generalized homological manifold and a homotopy manifold.

See also

• List of topologies
• Whitehead manifold, a contractible 3-manifold not homeomorphic to ${\displaystyle \mathbb {R} ^{3}}$.

References

• Daverman, Robert J. (2007), "Decompositions of manifolds", Geom. Topol. Monogr., 9: 7–15, arXiv:0903.3055, doi:10.1090/chel/362, ISBN 978-0-8218-4372-7, MR 2341468
• Bing, R. H. (1957), "A decomposition of E³ into points and tame arcs such that the decomposition space is topologically different from E³", Annals of Mathematics, Second Series, 65 (3): 484–500, doi:10.2307/1970058, ISSN 0003-486X, JSTOR 1970058, MR 0092961
• Bing, R. H. (1959), "The cartesian product of a certain nonmanifold and a line is E⁴", Annals of Mathematics, Second Series, 70 (3): 399–412, doi:10.2307/1970322, ISSN 0003-486X, JSTOR 1970322, MR 0107228