In chemistry, electro-osmotic flow (EOF, hyphen optional; synonymous with electro-osmosis or electro-endosmosis) is the motion of liquid induced by an applied potential across a porous material, capillary tube, membrane, microchannel, or any other fluid conduit. Because electro-osmotic velocities are independent of conduit size, as long as the electrical double layer is much smaller than the characteristic length scale of the channel, electro-osmotic flow will have little effect. Electro-osmotic flow is most significant when in small channels, and is an essential component in chemical separation techniques, notably capillary electrophoresis. Electro-osmotic flow can occur in natural unfiltered water, as well as buffered solutions.

Electro-osmotic flow schematic

History

Electro-osmotic flow was first reported in 1807 by Ferdinand Friedrich Reuss (18 February 1778 (Tübingen, Germany) – 14 April 1852 (Stuttgart, Germany))^[1] in an unpublished lecture before the Physical-Medical Society of Moscow;^[2] Reuss first published an account of electro-osmotic flow in 1809 in the Memoirs of the Imperial Society of Naturalists of Moscow.^[3][4] He showed that water could be made to flow through a plug of clay by applying an electric voltage. Clay is composed of closely packed particles of silica and other minerals, and water flows through the narrow spaces between these particles just as it would through a narrow glass tube. Any combination of an electrolyte (a fluid containing dissolved ions) and an insulating solid would generate electro-osmotic flow, though for water/silica the effect is particularly large. Even so, flow speeds are typically only a few millimeters per second.

Electro-osmosis was discovered independently in 1814 by the English chemist Robert Porrett Jr. (1783–1868).^[5][6]

Cause

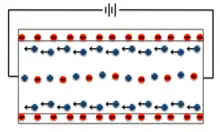
Electroosmotic flow is caused by the Coulomb force induced by an electric field on net mobile electric charge in a solution. Because the chemical equilibrium between a solid surface and an electrolyte solution typically leads to the interface acquiring a net fixed electrical charge, a layer of mobile ions, known as an electrical double layer or Debye layer, forms in the region near the interface. When an electric field is applied to the fluid (usually via electrodes placed at inlets and outlets), the net charge in the electrical double layer is induced to move by the resulting Coulomb force. The resulting flow is termed electroosmotic flow.

Description

The resulting flow from applying a voltage is a plug flow. Unlike a parabolic profile flow generated from a pressure differential, a plug flow’s velocity profile is approximately planar, with slight variation near the electric double layer. This offers significantly less deleterious dispersive effects and can be controlled without valves, offering a high-performance method for fluid separation, although many complex factors prove this control to be difficult. Because of difficulties measuring and monitoring flow in microfluidic channels, primarily disrupting the flow pattern, most analysis is done through numerical methods and simulation.^[7]

Electroosmotic flow through microchannels can be modeled after the Navier-Stokes equation with the driving force deriving from the electric field and the pressure differential. Thus it is governed by the continuity equation

${\displaystyle \nabla \cdot \mathbf {U} =0}$

and momentum

${\displaystyle \rho {\frac {D\mathbf {U} }{Dt}}=-\nabla p+\mu \nabla ^{2}\mathbf {U} +\rho _{e}\nabla \left(\psi +\phi \right),}$

where U is the velocity vector, ρ is the density of the fluid, ${\displaystyle D/Dt}$ is the material derivative, μ is the viscosity of the fluid, ρ_e is the electric charge density, ϕ is the applied electric field, ψ is the electric field due to the zeta potential at the walls and p is the fluid pressure.

Laplace’s equation can describe the external electric field

${\displaystyle \nabla ^{2}\phi =0,}$

while the potential within the electric double layer is governed by

${\displaystyle \nabla ^{2}\psi ={\frac {-\rho _{e}}{\epsilon \epsilon _{0}}},}$

where ε is the dielectric constant of the electrolyte solution and ε₀ is the vacuum permittivity. This equation can be further simplified using the Debye-Hückel approximation

${\displaystyle \nabla ^{2}\psi =k^{2}\psi ,}$

where 1 / k is the Debye length, used to describe the characteristic thickness of the electric double layer. The equations for potential field within the double layer can be combined as

${\displaystyle \rho _{e}=-\epsilon \epsilon _{0}k^{2}\psi .}$

The transport of ions in space can be modeled using the Nernst–Planck equation:^[8]

${\displaystyle {\partial c \over {\partial t}}=\nabla \cdot \left[D\nabla c-c{\bf {v}}+{Dze \over {k_{\text{B}}T}}c\left(\nabla \phi +{\partial {\bf {A}} \over {\partial t}}\right)\right]}$

Where ${\displaystyle \ c}$ is the ion concentration, ${\displaystyle {\bf {A}}}$ is the magnetic vector potential, ${\displaystyle D}$ is the diffusivity of the chemical species, ${\displaystyle z}$ is the valence of ionic species, ${\displaystyle e}$ is the elementary charge, ${\displaystyle k_{\text{B}}}$ is the Boltzmann constant, and ${\displaystyle T}$ is the absolute temperature.

Applications

Electro-osmotic flow is commonly used in microfluidic devices,^[9][10] soil analysis and processing,^[11] and chemical analysis,^[12] all of which routinely involve systems with highly charged surfaces, often of oxides. One example is capillary electrophoresis,^[10][12] in which electric fields are used to separate chemicals according to their electrophoretic mobility by applying an electric field to a narrow capillary, usually made of silica. In electrophoretic separations, the electroosmotic flow affects the elution time of the analytes.

Electro-osmotic flow is actuated in a FlowFET to electronically control fluid flow through a junction.

It is projected that micro fluidic devices utilizing electroosmotic flow will have applications in medical research. Once controlling this flow is better understood and implemented, the ability to separate fluids on the atomic level will be a vital component for drug dischargers.^[13] Mixing fluids at the micro scale is currently troublesome. It is believed that electrically controlling fluids will be the method in which small fluids are mixed.^[13]

A controversial use of electro-osmotic systems is the control rising damp in the walls of buildings.^[14] While there is little evidence to suggest that these systems can be useful in moving salts in walls, such systems are claimed to be especially effective in structures with very thick walls. However some claim that there is no scientific base for those systems, and cite several examples for their failure.^[15]

Electro-osmosis can also be used for self-pumping pores powered by chemical reactions rather than electric fields. This approach, using H₂O₂, has been demonstrated^[16] and modeled with the Nernst-Planck-Stokes equations.^[8]

Disadvantages

Maintaining an electric field in an electrolyte requires Faradaic reactions to occur at the anode and cathode. This is typically electrolysis of water, which generates hydrogen peroxide, hydrogen ions (acid) and hydroxide (base) as well as oxygen and hydrogen gas bubbles. The hydrogen peroxide and/or pH changes generated can adversely affect biological cells and biomolecules such as proteins, while gas bubbles tend to "clog" microfluidic systems. These problems can be alleviated by using alternative electrode materials such as conjugated polymers which can undergo the Faradaic reactions themselves, dramatically reducing electrolysis.^[19]

See also

Wikimedia Commons has media related to Electro-osmosis.

• Surface charge
• Capillary electrophoresis
• Electrical double layer
• Streaming current
• Induced-charge Electrokinetics
• Streaming potential
• Zeta potential
• Electroosmotic pump
• Electrical double layer
• Microfluidics
• Electrochemistry

References

Further reading

• Bell, F.G. (2000). Engineering Properties of Soils and Rocks, 4th ed.
• Chang, H.C.; Yao, L. (2009). Electrokinetically Driven Microfluidics and Nanofluidics.
• Levich, V. (1962). Physicochemical Hydrodynamics. ISBN 978-0-903012-40-9.
• Probstein, R.F. (2003). Physicochemical Hydrodynamics: an introduction, 2nd ed.