Equilibrant force

In mechanics, an equilibrant force is a force which brings a body into mechanical equilibrium.^[1] According to Newton's second law, a body has zero acceleration when the vector sum of all the forces acting upon it is zero:

${\displaystyle \sum \mathbf {F} =m\mathbf {a}$ ;\quad \sum \mathbf {F} =0\ \ \Rightarrow \ \ \mathbf {a} =0}

Therefore, an equilibrant force is equal in magnitude and opposite in direction to the resultant of all the other forces acting on a body. The term has been attested since the late 19th century.^[2]

Example

Equilibrant force example

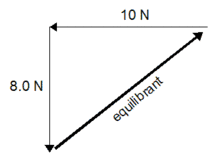
Suppose that two known forces, which are going to represented as vectors, A and B are pushing an object and an unknown equilibrant force, C, is acting to maintain that object in a fixed position. Force A points to the west and has a magnitude of 10 N and is represented by the vector <-10, 0>N. Force B points to the south and has a magnitude of 8.0 N and is represented by the vector <0, -8>N. Since these forces are vectors, they can be added by using the parallelogram rule^[3] or vector addition. This addition will look like A + B = <-10, 0>N + <0, -8>N = <-10, -8>N which is the vector representation of the resultant force. By the Pythagorean theorem, the magnitude of the resultant force is [(-10)² + (-8)²]^1/2 ≈ 12.8 N, which is also the magnitude of the equilibrant force. The angle of the equilibrant force can be found by trigonometry to be approximately 51 degrees north of east. Because the angle of the equilibrant force is opposite of the resultant force, if 180 degrees are added or subtracted to the resultant force's angle, the equilibrant force's angle will be known. Multiplying the resultant force vector by a -1 will give the correct equilibrant force vector: <-10, -8>N x (-1) = <10, 8>N = C.

References

External links

• Equilibrium