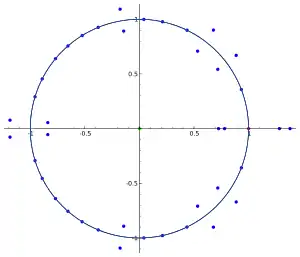
Roots of the Fekete polynomial for p = 43
In mathematics, a Fekete polynomial is a polynomial
where is the Legendre symbol modulo some integer p > 1.
These polynomials were known in nineteenth-century studies of Dirichlet L-functions, and indeed to Dirichlet himself. They have acquired the name of Michael Fekete, who observed that the absence of real zeroes t of the Fekete polynomial with 0 < t < 1 implies an absence of the same kind for the L-function
This is of considerable potential interest in number theory, in connection with the hypothetical Siegel zero near s = 1. While numerical results for small cases had indicated that there were few such real zeroes, further analysis reveals that this may indeed be a 'small number' effect.
References
- Peter Borwein: Computational excursions in analysis and number theory. Springer, 2002, ISBN 0-387-95444-9, Chap.5.
External links
- Brian Conrey, Andrew Granville, Bjorn Poonen and Kannan Soundararajan, Zeros of Fekete polynomials, arXiv e-print math.NT/9906214, June 16, 1999.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.