Generalized Maxwell model

Schematic of Maxwell–Wiechert model

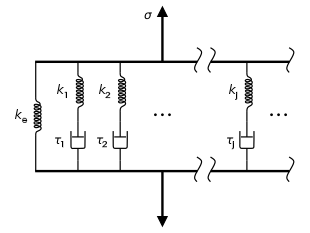
The Generalized Maxwell model also known as the Maxwell–Wiechert model (after James Clerk Maxwell and E Wiechert^[1]^[2]) is the most general form of the linear model for viscoelasticity. In this model several Maxwell elements are assembled in parallel. It takes into account that the relaxation does not occur at a single time, but in a set of times. Due to the presence of molecular segments of different lengths, with shorter ones contributing less than longer ones, there is a varying time distribution. The Wiechert model shows this by having as many spring–dashpot Maxwell elements as are necessary to accurately represent the distribution. The figure on the right shows the generalised Wiechert model.^[3]^[4]

General model form

Solids

Given $N+1$ elements with moduli $E_{i}$ , viscosities $\eta _{i}$ , and relaxation times $\tau _{i}={\frac {\eta _{i}}{E_{i}}}$

The general form for the model for solids is given by :

General Maxwell Solid Model (1)

$\sigma +$ $\sum _{n=1}^{N}{\left({\sum _{i_{1}=1}^{N-n+1}{...\left({\sum _{i_{a}=i_{a-1}+1}^{N-\left({n-a}\right)+1}{...\left({\sum _{i_{n}=i_{n-1}+1}^{N}{\left({\prod _{j\in \left\{{i_{1},...,i_{n}}\right\}}{\tau _{j}}}\right)}}\right)...}}\right)...}}\right){\frac {\partial ^{n}{\sigma }}{\partial {t}^{n}}}}$

$=$

$E_{0}\epsilon +$ $\sum _{n=1}^{N}{\left({\sum _{i_{1}=1}^{N-n+1}{...\left({\sum _{i_{a}=i_{a-1}+1}^{N-\left({n-a}\right)+1}{...\left({\sum _{i_{n}=i_{n-1}+1}^{N}{\left({\left({E_{0}+\sum _{j\in \left\{{i_{1},...,i_{n}}\right\}}{E_{j}}}\right)\left({\prod _{k\in \left\{{i_{1},...,i_{n}}\right\}}{\tau _{k}}}\right)}\right)}}\right)...}}\right)...}}\right){\frac {\partial ^{n}{\epsilon }}{\partial {t}^{n}}}}$

This may be more easily understood by showing the model in a slightly more expanded form:

General Maxwell Solid Model (2)

$\sigma +$ ${\left({\sum _{i=1}^{N}{\tau _{i}}}\right)}{\frac {\partial {\sigma }}{\partial {t}}}+$ ${\left({\sum _{i=1}^{N-1}{\left({\sum _{j=i+1}^{N}{\tau _{i}\tau _{j}}}\right)}}\right)}{\frac {\partial ^{2}{\sigma }}{\partial {t}^{2}}}$ $+...+$

$\left({\sum _{i_{1}=1}^{N-n+1}{...\left({\sum _{i_{a}=i_{a-1}+1}^{N-\left({n-a}\right)+1}{...\left({\sum _{i_{n}=i_{n-1}+1}^{N}{\left({\prod _{j\in \left\{{i_{1},...,i_{n}}\right\}}{\tau _{j}}}\right)}}\right)...}}\right)...}}\right){\frac {\partial ^{n}{\sigma }}{\partial {t}^{n}}}$ $+...+$ $\left({\prod _{i=1}^{N}{\tau _{i}}}\right){\frac {\partial ^{N}{\sigma }}{\partial {t}^{N}}}$

$=$

$E_{0}\epsilon +$ ${\left({\sum _{i=1}^{N}{\left({E_{0}+E_{i}}\right)\tau _{i}}}\right)}{\frac {\partial {\epsilon }}{\partial {t}}}+$ ${\left({\sum _{i=1}^{N-1}{\left({\sum _{j=i+1}^{N}{\left({E_{0}+E_{i}+E_{j}}\right)\tau _{i}\tau _{j}}}\right)}}\right)}{\frac {\partial ^{2}{\epsilon }}{\partial {t}^{2}}}$ $+...+$

$\left({\sum _{i_{1}=1}^{N-n+1}{...\left({\sum _{i_{a}=i_{a-1}+1}^{N-\left({n-a}\right)+1}{...\left({\sum _{i_{n}=i_{n-1}+1}^{N}{\left({\left({E_{0}+\sum _{j\in \left\{{i_{1},...,i_{n}}\right\}}{E_{j}}}\right)\left({\prod _{k\in \left\{{i_{1},...,i_{n}}\right\}}{\tau _{k}}}\right)}\right)}}\right)...}}\right)...}}\right){\frac {\partial ^{n}{\epsilon }}{\partial {t}^{n}}}$ $+...+$ $\left({E_{0}+\sum _{j=1}^{N}E_{j}}\right)\left({\prod _{i=1}^{N}{\tau _{i}}}\right){\frac {\partial ^{N}{\epsilon }}{\partial {t}^{N}}}$

Example: standard linear solid model

Following the above model with $N+1=2$ elements yields the standard linear solid model:

Standard Linear Solid Model (3)

$\sigma +\tau _{1}{\frac {\partial {\sigma }}{\partial {t}}}=E_{0}\epsilon +\tau _{1}\left({E_{0}+E_{1}}\right){\frac {\partial {\epsilon }}{\partial {t}}}$

Fluids

Given $N+1$ elements with moduli $E_{i}$ , viscosities $\eta _{i}$ , and relaxation times $\tau _{i}={\frac {\eta _{i}}{E_{i}}}$

The general form for the model for fluids is given by:

General Maxwell Fluid Model (4)

$\sigma +$ $\sum _{n=1}^{N}{\left({\sum _{i_{1}=1}^{N-n+1}{...\left({\sum _{i_{a}=i_{a-1}+1}^{N-\left({n-a}\right)+1}{...\left({\sum _{i_{n}=i_{n-1}+1}^{N}{\left({\prod _{j\in \left\{{i_{1},...,i_{n}}\right\}}{\tau _{j}}}\right)}}\right)...}}\right)...}}\right){\frac {\partial ^{n}{\sigma }}{\partial {t}^{n}}}}$

$=$

$\sum _{n=1}^{N}{\left({\eta _{0}+\sum _{i_{1}=1}^{N-n+1}{...\left({\sum _{i_{a}=i_{a-1}+1}^{N-\left({n-a}\right)+1}{...\left({\sum _{i_{n}=i_{n-1}+1}^{N}{\left({\left({\sum _{j\in \left\{{i_{1},...,i_{n}}\right\}}{E_{j}}}\right)\left({\prod _{k\in \left\{{i_{1},...,i_{n}}\right\}}{\tau _{k}}}\right)}\right)}}\right)...}}\right)...}}\right){\frac {\partial ^{n}{\epsilon }}{\partial {t}^{n}}}}$

This may be more easily understood by showing the model in a slightly more expanded form:

General Maxwell Fluid Model (5)

$\sigma +$ ${\left({\sum _{i=1}^{N}{\tau _{i}}}\right)}{\frac {\partial {\sigma }}{\partial {t}}}+$ ${\left({\sum _{i=1}^{N-1}{\left({\sum _{j=i+1}^{N}{\tau _{i}\tau _{j}}}\right)}}\right)}{\frac {\partial ^{2}{\sigma }}{\partial {t}^{2}}}$ $+...+$

$\left({\sum _{i_{1}=1}^{N-n+1}{...\left({\sum _{i_{a}=i_{a-1}+1}^{N-\left({n-a}\right)+1}{...\left({\sum _{i_{n}=i_{n-1}+1}^{N}{\left({\prod _{j\in \left\{{i_{1},...,i_{n}}\right\}}{\tau _{j}}}\right)}}\right)...}}\right)...}}\right){\frac {\partial ^{n}{\sigma }}{\partial {t}^{n}}}$ $+...+$ $\left({\prod _{i=1}^{N}{\tau _{i}}}\right){\frac {\partial ^{N}{\sigma }}{\partial {t}^{N}}}$

$=$

${\left({\eta _{0}+\sum _{i=1}^{N}{E_{i}\tau _{i}}}\right)}{\frac {\partial {\epsilon }}{\partial {t}}}+$ ${\left({\eta _{0}+\sum _{i=1}^{N-1}{\left({\sum _{j=i+1}^{N}{\left({E_{i}+E_{j}}\right)\tau _{i}\tau _{j}}}\right)}}\right)}{\frac {\partial ^{2}{\epsilon }}{\partial {t}^{2}}}$ $+...+$

$\left({\eta _{0}+\sum _{i_{1}=1}^{N-n+1}{...\left({\sum _{i_{a}=i_{a-1}+1}^{N-\left({n-a}\right)+1}{...\left({\sum _{i_{n}=i_{n-1}+1}^{N}{\left({\left({\sum _{j\in \left\{{i_{1},...,i_{n}}\right\}}{E_{j}}}\right)\left({\prod _{k\in \left\{{i_{1},...,i_{n}}\right\}}{\tau _{k}}}\right)}\right)}}\right)...}}\right)...}}\right){\frac {\partial ^{n}{\epsilon }}{\partial {t}^{n}}}$ $+...+$ $\left({\eta _{0}+\left({\sum _{j=1}^{N}E_{j}}\right)\left({\prod _{i=1}^{N}{\tau _{i}}}\right)}\right){\frac {\partial ^{N}{\epsilon }}{\partial {t}^{N}}}$

Example: three parameter fluid

The analogous model to the standard linear solid model is the three parameter fluid, also known as the Jeffreys model:^[5]

Three Parameter Maxwell Fluid Model (6)

$\sigma +\tau _{1}{\frac {\partial {\sigma }}{\partial {t}}}=\left({\eta _{0}+\tau _{1}E_{1}{\frac {\partial }{\partial t}}}\right){\frac {\partial {\epsilon }}{\partial {t}}}$

References

↑ Wiechert, E (1889); "Ueber elastische Nachwirkung", Dissertation, Königsberg University, Germany
↑ Wiechert, E (1893); "Gesetze der elastischen Nachwirkung für constante Temperatur", Annalen der Physik, Vol. 286, issue 10, p. 335–348 and issue 11, p. 546–570
↑ Roylance, David (2001); "Engineering Viscoelasticity", 14-15
↑ Tschoegl, Nicholas W. (1989); "The Phenomenological Theory of Linear Viscoelastic Behavior", 119-126
↑ Gutierrez-Lemini, Danton (2013). Engineering Viscoelasticity. Springer. p. 88. ISBN 9781461481393.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[Wiechert1-1] Wiechert, E (1889); "Ueber elastische Nachwirkung", Dissertation, Königsberg University, Germany

[Wiechert2-2] Wiechert, E (1893); "Gesetze der elastischen Nachwirkung für constante Temperatur", Annalen der Physik, Vol. 286, issue 10, p. 335–348 and issue 11, p. 546–570

[Roylance-3] Roylance, David (2001); "Engineering Viscoelasticity", 14-15

[Tschoegl-4] Tschoegl, Nicholas W. (1989); "The Phenomenological Theory of Linear Viscoelastic Behavior", 119-126

[5] Gutierrez-Lemini, Danton (2013). Engineering Viscoelasticity. Springer. p. 88. ISBN 9781461481393.

[1]

[2]

[3]

[4]

[5]