In graph theory, a geodetic graph is an undirected graph such that there exists a unique (unweighted) shortest path between each two vertices.

Geodetic graphs were introduced in 1962 by Øystein Ore, who observed that they generalize a property of trees (in which there exists a unique path between each two vertices regardless of distance), and asked for a characterization of them.^[1] Although these graphs can be recognized in polynomial time, "more than sixty years later a full characterization is still elusive".^[2]

Examples

Every tree,^[1] every complete graph,^[3] and every odd-length cycle graph is geodetic.^[4]

If ${\displaystyle G}$ is a geodetic graph, then replacing every edge of ${\displaystyle G}$ by a path of the same odd length will produce another geodetic graph.^[5] In the case of a complete graph, a more general pattern of replacement by paths is possible: choose a non-negative integer ${\displaystyle f(v)}$ for each vertex ${\displaystyle v}$, and subdivide each edge ${\displaystyle uv}$ by adding ${\displaystyle f(u)+f(v)}$ vertices to it. Then the resulting subdivided complete graph is geodetic, and every geodetic subdivided complete graph can be obtained in this way.^[6][7]

Related graph classes

A block graph, a special case of a geodetic graph

The Petersen graph, one of the geodetic graphs of diameter two

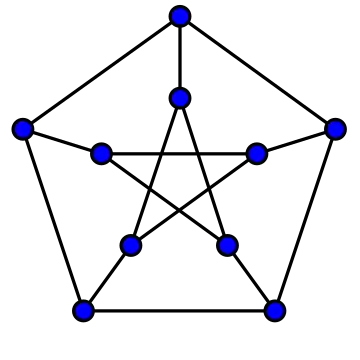
If every biconnected component of a graph is geodetic then the graph itself is geodetic. In particular, every block graph (graphs in which the biconnected components are complete) is geodetic.^[3] Similarly, because a cycle graph is geodetic when it has odd length, every cactus graph in which the cycles have odd length is also geodetic. These cactus graphs are exactly the connected graphs in which all cycles have odd length. More strongly, a planar graph is geodetic if and only if all of its biconnected components are either odd-length cycles or geodetic subdivisions of a four-vertex clique.^[4]

Computational complexity

Geodetic graphs may be recognized in polynomial time, by using a variation of breadth first search that can detect multiple shortest paths, starting from each vertex of the graph. Geodetic graphs cannot contain an induced four-vertex cycle graph, nor an induced diamond graph, because these two graphs are not geodetic.^[3] In particular, as a subset of diamond-free graphs, the geodetic graphs have the property that every edge belongs to a unique maximal clique; in this context, the maximal cliques have also been called lines.^[8] It follows that the problem of finding maximum cliques, or maximum weighted cliques, can be solved in polynomial time for geodetic graphs, by listing all maximal cliques. The broader class of graphs that have no induced 4-cycle or diamond are called "weakly geodetic"; these are the graphs where vertices at distance exactly two from each other have a unique shortest path.^[3]

Diameter two

For graphs of diameter two (that is, graphs in which all vertices are at distance at most two from each other), the geodetic graphs and weakly geodetic graphs coincide. Every geodetic graph of diameter two is of one of three types:

• a block graph in which all the maximal cliques are joined at a single shared vertex, including the windmill graphs,
• a strongly regular graph with parameter ${\displaystyle \mu }$ (the number of shared neighbors for each nonadjacent pair of vertices) equal to one, or
• a graph with exactly two different vertex degrees.

The strongly regular geodetic graphs include the 5-vertex cycle graph, the Petersen graph, and the Hoffman–Singleton graph. Despite additional research on the properties such a graph must have,^[9][10] it is not known whether there are more of these graphs, or infinitely many of these graphs.^[8]

Geodetic graphs with diameter two and two different degrees cannot have a triangle composed of vertices of both degrees. They can be constructed from any finite affine plane by adding to the point-line incidence graph of the plane additional edges between the vertices corresponding to each two parallel lines. For the binary affine plane with four points and six two-point lines in three parallel pairs, the result of this construction is the Petersen graph, but for higher-order finite affine planes it produces graphs with two different degrees. Other related constructions of geodetic graphs from finite geometries are also known, but it is not known whether these exhaust all the possible geodetic graphs with diameter two and two different degrees.^[8]

References