In combinatorial optimization, the Gomory–Hu tree[1] of an undirected graph with capacities is a weighted tree that represents the minimum s-t cuts for all s-t pairs in the graph. The Gomory–Hu tree can be constructed in |V| − 1 maximum flow computations. It is named for Ralph E. Gomory and T. C. Hu.
Definition
Let be an undirected graph with being the capacity of the edge respectively.
- Denote the minimum capacity of an s-t cut by for each .
- Let be a tree, and denote the set of edges in an s-t path by for each .
Then T is said to be a Gomory–Hu tree of G, if for each
where
- are the two connected components of , and thus forms an s-t cut in G.
- is the capacity of the cut in G.
Algorithm
Gomory–Hu Algorithm
- Input: A weighted undirected graph
- Output: A Gomory–Hu Tree
- Set
- Choose some with |X| ≥ 2 if such X exists. Otherwise, go to step 6.
- For each connected component let
- Let
- Contract the components to form where:
- is the capacity function, defined as:
- is the capacity function, defined as:
- Choose two vertices s, t ∈ X and find a minimum s-t cut (A′, B′) in G'.
- Set
- Set
- For each do:
- Set if otherwise set
- Set
- Set
- Set
- Set
- Go to step 2.
- For each do:
- Replace each by v and each by (u, v). Output T.
Analysis
Using the submodular property of the capacity function c, one has
Then it can be shown that the minimum s-t cut in G' is also a minimum s-t cut in G for any s, t ∈ X.
To show that for all for some p ∈ P, q ∈ Q throughout the algorithm, one makes use of the following Lemma,
- For any i, j, k in VG,
The Lemma can be used again repeatedly to show that the output T satisfies the properties of a Gomory–Hu Tree.
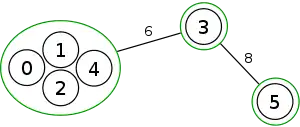
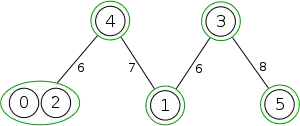
Example
The following is a simulation of the Gomory–Hu's algorithm, where
- green circles are vertices of T.
- red and blue circles are the vertices in G'.
- grey vertices are the chosen s and t.
- red and blue coloring represents the s-t cut.
- dashed edges are the s-t cut-set.
- A is the set of vertices circled in red and B is the set of vertices circled in blue.
| G' | T | |
|---|---|---|
 |
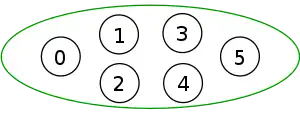 | |
| ||
| 1. | 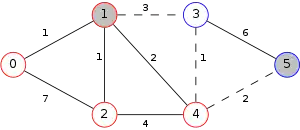 |
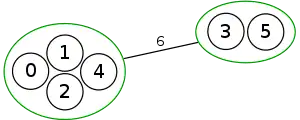 |
| ||
| 2. | 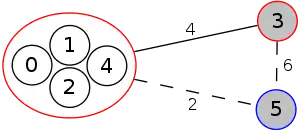 |
 |
| ||
| 3. | 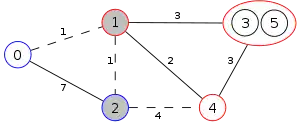 |
 |
| ||
| 4. |  |
 |
| ||
| 5. | 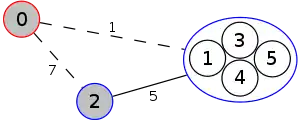 |
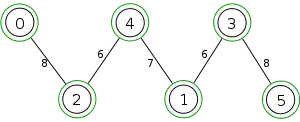 |
| ||
| 6. |
| |
| ||
Implementations: Sequential and Parallel
Gusfield's algorithm can be used to find a Gomory–Hu tree without any vertex contraction in the same running time-complexity, which simplifies the implementation of constructing a Gomory–Hu Tree.[2]
Andrew V. Goldberg and K. Tsioutsiouliklis implemented the Gomory-Hu algorithm and Gusfield algorithm, and performed an experimental evaluation and comparison.[3]
Cohen et al. report results on two parallel implementations of Gusfield's algorithm using OpenMP and MPI, respectively.[4]
Related concepts
In planar graphs, the Gomory–Hu tree is dual to the minimum weight cycle basis, in the sense that the cuts of the Gomory–Hu tree are dual to a collection of cycles in the dual graph that form a minimum-weight cycle basis.[5]
See also
References
- ↑ Gomory, R. E.; Hu, T. C. (1961). "Multi-terminal network flows". Journal of the Society for Industrial and Applied Mathematics. 9 (4): 551–570. doi:10.1137/0109047.
- ↑ Gusfield, Dan (1990). "Very Simple Methods for All Pairs Network Flow Analysis". SIAM J. Comput. 19 (1): 143–155. doi:10.1137/0219009.
- ↑ Goldberg, A. V.; Tsioutsiouliklis, K. (2001). "Cut Tree Algorithms: An Experimental Study". Journal of Algorithms. 38 (1): 51–83. doi:10.1006/jagm.2000.1136.
- ↑ Cohen, Jaime; Rodrigues, Luiz A.; Silva, Fabiano; Carmo, Renato; Guedes, André Luiz Pires; Duarte, Jr., Elias P. (2011). "Parallel implementations of Gusfield's cut tree algorithm". In Xiang, Yang; Cuzzocrea, Alfredo; Hobbs, Michael; Zhou, Wanlei (eds.). Algorithms and Architectures for Parallel Processing – 11th International Conference, ICA3PP, Melbourne, Australia, October 24–26, 2011, Proceedings, Part I. Lecture Notes in Computer Science. Vol. 7016. Springer. pp. 258–269. doi:10.1007/978-3-642-24650-0_22.
{{cite conference}}: CS1 maint: multiple names: authors list (link) - ↑ Hartvigsen, D.; Mardon, R. (1994). "The all-pairs min cut problem and the minimum cycle basis problem on planar graphs". SIAM J. Discrete Math. 7 (3): 403–418. doi:10.1137/S0895480190177042..
- B. H. Korte, Jens Vygen (2008). "8.6 Gomory–Hu Trees". Combinatorial Optimization: Theory and Algorithms (Algorithms and Combinatorics, 21). Springer Berlin Heidelberg. pp. 180–186. ISBN 978-3-540-71844-4.
