In Euclidean geometry, a harmonic quadrilateral, or harmonic quadrangle,[1] is a quadrilateral that can be inscribed in a circle (cyclic quadrangle) in which the products of the lengths of opposite sides are equal. It has several important properties.
Properties
Let ABCD be a harmonic quadrilateral and M the midpoint of diagonal AC. Then:
- Tangents to the circumscribed circle at points A and C and the straight line BD either intersect at one point or are mutually parallel.
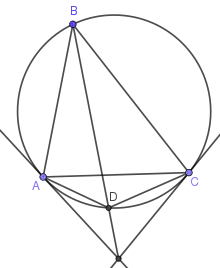
Tangents to the circumscribed circle at points A and C and the straight line BD either intersect at one point or are mutually parallel.
- Angles ∠BMC and ∠DMC are equal.

Angles ∠BMC and ∠DMC are equal.
- The bisectors of the angles at B and D intersect on the diagonal AC.
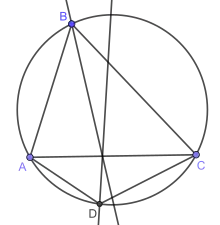
The bisectors of the angles at B and D intersect on the diagonal AC.
- A diagonal BD of the quadrilateral is a symmedian of the angles at B and D in the triangles ∆ABC and ∆ADC.
- The point of intersection of the diagonals is located towards the sides of the quadrilateral to proportional distances to the length of these sides.
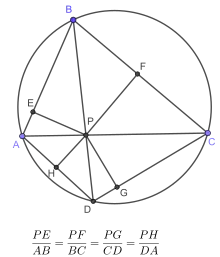
The point of intersection of the diagonals is located towards the sides of the quadrilateral to proportional distances to the length of these sides.
References
Further reading
- Gallatly, W. "The Harmonic Quadrilateral." §124 in The Modern Geometry of the Triangle, 2nd ed. London: Hodgson, pp. 90 and 92, 1913.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.