In particle physics, a hyperon is any baryon containing one or more strange quarks, but no charm, bottom, or top quark.[1] This form of matter may exist in a stable form within the core of some neutron stars.[2] Hyperons are sometimes generically represented by the symbol Y.[3]

History and research

The first research into hyperons happened in the 1950s and spurred physicists on to the creation of an organized classification of particles.

The term was coined by French physicist Louis Leprince-Ringuet in 1953,[4][5] and announced for the first time at the cosmic ray conference at Bagnères de Bigorre in July of that year, agreed upon by Leprince-Ringuet, Bruno Rossi, C.F. Powell, William B. Fretter and Bernard Peters.[6]

Today, research in this area is carried out on data taken at many facilities around the world, including CERN, Fermilab, SLAC, JLAB, Brookhaven National Laboratory, KEK, GSI and others. Physics topics include searches for CP violation, measurements of spin, studies of excited states (commonly referred to as spectroscopy), and hunts for exotic forms such as pentaquarks and dibaryons.

Properties and behavior

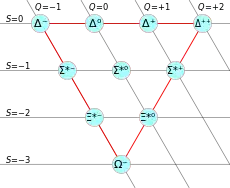
A combination of three u, d or s-quarks with a total spin of 3/2 form the so-called baryon decuplet. The lower six are hyperons.

Being baryons, all hyperons are fermions. That is, they have half-integer spin and obey Fermi–Dirac statistics. Hyperons all interact via the strong nuclear force, making them types of hadron. They are composed of three light quarks, at least one of which is a strange quark, which makes them strange baryons.

Excited hyperon resonances and ground-state hyperons with a '*' included in their notation decay via the strong interaction. For Ω⁻ as well as the lighter hyperons this decay mode is not possible given the particle masses and the conservation of flavor and isospin necessary in strong interactions. Instead, these decay weakly with non-conserved parity. An exception to this is the Σ⁰ which decays electromagnetically into Λ on account of carrying the same flavor quantum numbers. The type of interaction through which these decays occur determine the average lifetime, which is why weakly decaying hyperons are significantly more long-lived than those that decay through strong or electromagnetic interactions.[7]

List

Hyperons
Particle Symbol Makeup Rest mass
(MeV/c2)		 Isospin,
I		 Spin, parity,
JP		 Q
(e)		 S C B' Mean lifetime
(s)		 Commonly
decays to
Lambda[8]
Λ0
u

d

s
 1 115.683(6) 0 1⁄2+ 0 −1 0 0 2.60×10−10[9]
p+
 +
π−
 or

n0
 +
π0
Lambda resonance[10]
Λ
(1405)
u

d

s
 1 405.1(+1.3 -1.0) 0 1⁄2− 0 −1 0 0
Σ
 +
π
Lambda resonance[11]
Λ
(1520)
u

d

s
 1 519(1) 0 3⁄2− 0 −1 0 0
N
 +
K
 or
Σ
 +
π
 or
Λ
 + 2
π
Sigma[12]
Σ+
u

u

s
 1 189.37(7) 1 1⁄2+ +1 −1 0 0 (8.018±0.026)×10−11
p+
 +
π0
 or

n0
 +
π+
Sigma[13]
Σ0
u

d

s
 1 192.642(24) 1 1⁄2+ 0 −1 0 0 (7.4±0.7)×10−20
Λ0
 +
γ
Sigma[14]
Σ−
d

d

s
 1 197.449(30) 1 1⁄2+ −1 −1 0 0 (1.479±0.011)×10−10
n0
 +
π−
Sigma resonance[15]
Σ∗+
(1385)
u

u

s
 1 382.8(4) 1 3⁄2+ +1 −1 0 0
Λ
 +
π
 or

Σ
 +
π
Sigma resonance[15]
Σ∗0
(1385)
u

d

s
 1 383.7±1.0 1 3⁄2+ 0 −1 0 0
Λ
 +
π
 or

Σ
 +
π
Sigma resonance[15]
Σ∗−
(1385)
d

d

s
 1 387.2(5) 1 3⁄2+ −1 −1 0 0
Λ
 +
π
 or

Σ
 +
π
Xi[16]
Ξ0
u

s

s
 1 314.86(20) 1⁄2 1⁄2+ 0 −2 0 0 (2.90±0.09)×10−10
Λ0
 +
π0
Xi[17]
Ξ−
d

s

s
 1 321.71(7) 1⁄2 1⁄2+ −1 −2 0 0 (1.639±0.015)×10−10
Λ0
 +
π−
Xi resonance[18]
Ξ∗0
(1530)
u

s

s
 1 531.80(32) 1⁄2 3⁄2+ 0 −2 0 0
Ξ
 +
π
Xi resonance[18]
Ξ∗−
(1530)
d

s

s
 1 535.0(6) 1⁄2 3⁄2+ −1 −2 0 0
Ξ
 +
π
Omega[19]
Ω−
s

s

s
 1 672.45(29) 0 3⁄2+ −1 −3 0 0 (8.21±0.11)×10−11
Λ0
 +
K−
 or

Ξ0
 +
π−
 or

Ξ−
 +
π0

Notes:

  • Since strangeness is conserved by the strong interactions, some ground-state hyperons cannot decay strongly. However, they do participate in strong interactions.

  • Λ0
     may also decay on rare occurrences via these processes:

    Λ0
     →
    p+
     +
    e−
     +
    ν
    e

    Λ0
     →
    p+
     +
    μ−
     +
    ν
    μ

  • Ξ0
     and
    Ξ−
     are also known as "cascade" hyperons, since they go through a two-step cascading decay into a nucleon.
  • The
    Ω−
     has a baryon number of +1 and hypercharge of −2, giving it strangeness of −3. It takes multiple flavor-changing weak decays for it to decay into a proton or neutron. Murray Gell-Mann's and Yuval Ne'eman's SU(3) model (sometimes called the Eightfold Way) predicted this hyperon's existence, mass and that it will only undergo weak decay processes. Experimental evidence for its existence was discovered in 1964 at Brookhaven National Laboratory. Further examples of its formation and observation using particle accelerators confirmed the SU(3) model.

See also

Look up hyperon in Wiktionary, the free dictionary.

References

  1. ↑ Greiner, Walter (2001). "Structure of vacuum and elementary matter: from superheavies via hypermatter to antimatter.". In Arias, J.M.; Lozano, M. (eds.). An Advanced Course in Modern Nuclear Physics. Lecture Notes in Physics. Vol. 581. pp. 316–342. doi:10.1007/3-540-44620-6_11. ISBN 978-3-540-42409-3.
  2. ↑ Schaffner-Bielich, Jürgen; et al. (2002), "Phase Transition to Hyperon Matter in Neutron Stars", Physical Review Letters, 89 (17): 171101, arXiv:astro-ph/0005490, Bibcode:2002PhRvL..89q1101S, doi:10.1103/PhysRevLett.89.171101, PMID 12398654, S2CID 18759347, 171101
  3. ↑ Tolos, L.; Fabbietti, L. (May 2020). "Strangeness in nuclei and neutron stars". Progress in Particle and Nuclear Physics. 112: 41. arXiv:2002.09223. Bibcode:2020PrPNP.11203770T. doi:10.1016/j.ppnp.2020.103770. S2CID 211252559.
  4. ↑ Degrange, Bernard; Fontaine, Gérard; Fleury, Patrick (2013). "Tracking Louis Leprince-Ringuet's contributions to cosmic-ray physics". Physics Today. 66 (6): 8. Bibcode:2013PhT....66f...8D. doi:10.1063/PT.3.1989. ISSN 0031-9228.
  5. ↑ Ravel, Olivier (2013). Ormes, Jonathan F. (ed.). Early cosmic ray research in France. Centenary Symposium 2012: Discovery of Cosmic Rays. AIP Conference Proceedings. Vol. 1516. Denver, United States: American Institute of Physics. pp. 67–71. Bibcode:2013AIPC.1516...67R. doi:10.1063/1.4792542. ISBN 978-0-7354-1137-1.
  6. ↑ J.W. Cronin (2011). "The 1953 Cosmic Ray Conference at Bagnères de Bigorre: the Birth of Sub Atomic Physics". The European Physical Journal H. 36 (2): 183–201. arXiv:1111.5338. Bibcode:2011EPJH...36..183C. doi:10.1140/epjh/e2011-20014-4. S2CID 119105540. See in particular Fig. 5.
  7. ↑ Martin, B. R. (2017). Particle physics (Fourth ed.). Chichester, West Sussex, United Kingdom. ISBN 9781118911907.{{cite book}}: CS1 maint: location missing publisher (link)
  8. ↑ "Particle Data Groups: 2006 Review of Particle Physics – Lambda" (PDF). Archived from the original (PDF) on 2008-09-10. Retrieved 2008-04-20.
  9. ↑ "Physics Particle Overview – Baryons". Archived from the original on 2008-02-28. Retrieved 2008-04-20.
  10. ↑ "Particle Data Groups: 2006 Review of Particle Physics – Lambda" (PDF). Archived from the original (PDF) on 2008-09-10. Retrieved 2008-04-20.
  11. ↑ "Particle Data Groups: 2006 Review of Particle Physics – Lambda" (PDF). Archived from the original (PDF) on 2008-09-10. Retrieved 2008-04-20.
  12. ↑ "Particle Data Groups: 2006 Review of Particle Physics – Sigma+" (PDF). Archived from the original (PDF) on 2008-09-10. Retrieved 2008-04-20.
  13. ↑ "Particle Data Groups: 2006 Review of Particle Physics – Sigma0" (PDF). Archived from the original (PDF) on 2008-09-10. Retrieved 2008-04-20.
  14. ↑ "Particle Data Groups: 2006 Review of Particle Physics – Sigma-" (PDF). Archived from the original (PDF) on 2008-09-10. Retrieved 2008-04-20.
  15. 1 2 3 "Particle Data Groups: 2006 Review of Particle Physics – Sigma(1385)" (PDF). Archived from the original (PDF) on 2008-09-10. Retrieved 2008-04-20.
  16. ↑ "Particle Data Groups: 2006 Review of Particle Physics – Xi0" (PDF). Retrieved 2008-04-20.
  17. ↑ "Particle Data Groups: 2006 Review of Particle Physics – Xi-" (PDF). Retrieved 2008-04-20.
  18. 1 2 "Particle Data Groups: 2006 Review of Particle Physics – Xi(1530)" (PDF). Retrieved 2008-04-20.
  19. ↑ "Particle Data Groups: 2006 Review of Particle Physics – Omega-" (PDF). Retrieved 2008-04-20.
  • Semat, Henry; Albright, John R. (1984). Introduction to Atomic and Nuclear Physics. Chapman and Hall. ISBN 0-412-15670-9.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.