In the height region between about 85 and 200 km altitude on Earth, the ionospheric plasma is electrically conducting. Atmospheric tidal winds due to differential solar heating or due to gravitational lunar forcing move the ionospheric plasma against the geomagnetic field lines thus generating electric fields and currents just like a dynamo coil moving against magnetic field lines. That region is therefore called ionospheric dynamo region.[1] The magnetic manifestation of these electric currents on the ground can be observed during magnetospheric quiet conditions. They are called Sq-variations (S=solar; q=quiet) and L-variations (L=lunar) of the geomagnetic field. Additional electric currents are generated by the varying magnetospheric electric convection field. These are the DP1-currents (the auroral electrojets) and the polar DP2-currents. [2] Finally, a polar-ring current has been derived from the observations which depends on the polarity of the interplanetary magnetic field.[3] These geomagnetic variations belong to the so-called external part of the geomagnetic field. Their amplitudes reach at most about 1% of the main internal geomagnetic field Bo.
Atmospheric electric conductivity
Radioactive material from the ground and galactic cosmic rays ionize a small fraction of the atmospheric gas within the lower and middle atmosphere and make the gas electrically conducting. Electrons quickly attach to neutral particles forming negative ions. The positive ions are mostly singly charged. The electric conductivity depends on the mobility of the ions . That mobility is proportional to the reciprocal air density. Thus, the electric conductivity increases almost exponentially with altitude. The ions move with the neutral gas making the conductivity isotropic.[4]
At heights between about 85 and 200 km however -the dynamo region-, solar X- and extreme ultraviolet radiation (XUV) is almost completely absorbed generating the ionospheric D-, E-, and F-layers. Here, the electrons are already bound to the geomagnetic field gyrating several times about these lines before they collide with the neutrals, while the positive ions still essentially move with the neutral gas. Thus, the electric conductivity becomes anisotropic. The conductivity parallel to an electric field E is called Pedersen conductivity. The conductivity orthogonal to E and the geomagnetic field Bo is the Hall conductivity. Ohmic losses and thus Joule heating occur when Pedersen currents flow. The component parallel to Bo still increases with altitude. Near the geomagnetic dip equator, a west–east directed electric field generates vertical Hall currents which cannot close. Therefore, a vertical polarization field builds up generating a horizontal Hall current which adds to the Pedersen current. Such enhancement is described by the Cowling conductivity. Pedersen and Hall conductivities reach maximum values near 120 to 140 km altitudes with numbers of about 1 mS/m during sunlit conditions. During the night, these numbers may decrease by a factor of ten or more. The values of these conductivities depend on local time, latitude, season and solar 11- year cycle. The height integrated conductivities become of the order of 50 S, or a total resistance of the dynamo region of about 1/50 = 0.02 Ohm during daytime conditions.[5]
In the auroral regions which lie between about 15° and 20° geomagnetic co-latitude and the corresponding latitudes in the southern hemisphere, precipitating high energy particles from the magnetosphere ionize the neutral gas, in particular at heights around 110 to 120 km, and increase the electric conductivity substantially. During magnetospheric disturbed conditions, this conductivity enhancement becomes much larger, and the auroral regions move equatorward.[2]
At heights above about 200 km, collisions between neutrals and plasma become rare so that both ions and electrons can only gyrate about the geomagnetic lines of force, or drift orthogonal to E and Bo. The parallel conductivity is so large that the geomagnetic lines of force become electric potential lines, and only electric fields orthogonal to Bo can exist (see magnetosphere).
Atmospheric tides
Atmospheric tides are global-scale waves excited by regular solar differential heating (thermal tides) or by the gravitational tidal force of the Moon (gravitational tides). The atmosphere behaves like a huge waveguide closed at the bottom (the Earth's surface) and open to space at the top. In such a waveguide an infinite number of atmospheric wave modes can be excited. Because the waveguide is imperfect, however, only modes of lowest degree with large horizontal and vertical scales can develop sufficiently well so that they can be filtered out from the meteorological noise. They are solutions of the Laplace equation [6] and are called Hough functions. These can be approximated by a sum of spherical harmonics.
Two kinds of wave modes exist: class 1 waves (sometimes called gravity waves), and class 2 waves (rotational waves). Class 2 waves owe their existence to the Coriolis effect and can only exist for periods larger than 12 hours. Tidal waves can be either internal (travelling waves) with positive eigenvalues (or equivalent depth) which have finite vertical wavelengths and can transport wave energy upward, or external (evanescent waves) with negative eigenvalues and infinitely large vertical wavelengths meaning that their phases remain constant with altitude. These external wave modes cannot transport wave energy, and their amplitudes decrease exponentially with height outside their source regions. Each mode is characterized by four numbers: the zonal wave number n, positive for class 1 waves and negative for class 2 waves (their meridional structures becoming increasingly complex with increasing number n), a meridional wave number m, the eigenvalue, and the period, in our case one solar or lunar day, respectively. The modes are labeled as (m, n). Even numbers of n correspond to waves symmetric with respect to the equator, and odd numbers corresponding to antisymmetric waves.
At thermospheric heights, dissipation of atmospheric waves becomes significant so that at above about 150 km altitude, all wave modes gradually become external waves, and the Hough functions degenerate to spherical harmonics; e.g., mode (1, -2) develops to the spherical harmonic P11(θ), mode (2, 2) becomes P22(θ), with θ the co-latitude, etc.[7] Atmospheric tides are observed by radars within and above the ionospheric dynamo region in thermosphere, and can be simulated by general circulation models, though the excitation mechanisms of these tides are currently under debate. [8]
Migrating solar tides
The fundamental solar diurnal tidal mode that optimally matches the solar heat input configuration and thus is most strongly excited is the (1, -2) - mode. It depends on local time and travels westward with the Sun. It is an external mode of class 2. Its maximum pressure amplitude on the ground is about 60 hPa.[9] Within the thermosphere, however, it becomes the predominant mode, reaching temperature amplitudes at the exosphere of at least 140 K and horizontal winds of the order of 100 m/s and more increasing with geomagnetic activity.[10] The largest solar semidiurnal wave is mode (2, 2) with maximum pressure amplitudes near the ground of 120 hPa. It is an internal class 1 wave. Its amplitude increases with altitude. Although its solar excitation is half of that of mode (1, -2), its amplitude on the ground is larger by a factor of two. This indicates the effect of suppression of external waves, in this case by a factor of four.[7]
Semidiurnal lunar tides
The dominant migrating lunar tide is the (2, 2) mode depending on lunar local time. Its maximum pressure amplitude near the ground is 6 Pa, which is far below the meteorological noise. Therefore, it is not simple to detect such a small signal.[9] Because it is an internal waves, its amplitude increases with altitude, reaching values at 100 km height two orders of magnitude larger than on the ground.
Electric currents
Sq-Current
Morphology
More than 100 geomagnetic observatories around the world measure regularly the variations of the Earth's magnetic field. The daily variations during selected days of quiet geomagnetic activity are used to determine a monthly mean. From the horizontal component ΔH of such data, one can derive a corresponding overhead equivalent electric sheet current system at dynamo layer heights of strength
J = 2 ΔH/μ = 1.6 ΔH
with J (in milliAmpere/meter) the electric overhead sheet current, ΔH (in nanoTesla) the observed horizontal component of the geomagnetic variation, and μ the electric permeability of free space.[1] One can determine the direction of the magnetic field with regard to the current by the simple rule of thumb: if the thumb of the right hand points into the direction of the current, the curved fingers give the direction of the associated magnetic field.
One has to take into account that this relationship is not unique. In general, electric currents within ionosphere and magnetosphere are three-dimensional, and an infinite number of current configurations fits to the geomagnetic variations observed on the ground.[11] Magnetic measurement in space are necessary to obtain a realistic picture.
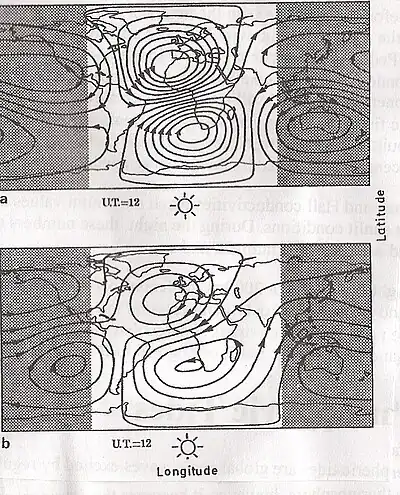
Figure 1a shows current streamlines of an equivalent Sq current as seen from the Sun at noon. This current configuration is fixed to the Sun, while the Earth rotates beneath it. A total current of about 140 kA flows within one daytime vortex. The rotating Sq current and the electrically conducting Earth interior behave like a huge transformer with the dynamo region as the primary winding and the Earth as the secondary winding. Since the Sq current varies with the basic period of one day, electric currents are induced within the Earth's interior. The magnetic field of this secondary current is superimposed on the magnetic field of the primary Sq current. Methods to separate both components go back to Gauss. The amplitude of the secondary current is about 1/3 of that of the primary current and slightly shifted in phase. Figure 1b shows that secondary component. The ratio between sheet current and magnetic component given above has now simply the value one.
The Sq current depends on season. The summer vortex is intensified compared with the winter vortex and reaches into the winter hemisphere. A longitudinal dependence of the Sq current exists which is related to the inclined dipole component of the internal magnetic field, but probably also to nonmigrating tidal waves from below.[13] In the course of the 11-year solar cycle, the amplitude of Sq increases by a factor of more than two from sunspot minimum to sunspot maximum. Two thirds of this increase may result from the enhancement of the electric conductivity with solar activity. The rest is probably due to the increase of the wind speed caused by the temperature increase with increasing solar activity. During the night, the electron density of the ionospheric E-layer diminishes much more strongly than that of the F-layer. Therefore, the height center of the dynamo region shifts upward.[14]
The main driver of the Sq current is the external (1, -2) tidal wave mode. Due to its constant phase with altitude, is most efficient to drive coherent winds at dynamo layer height,[15] while the currents generated by the internal modes interfere destructively at various heights.[16] A Fourier analysis shows a semidiurnal component with an amplitude of 1 /2 of that of the diurnal component, phase shifted by 180°. This appears to be the result of nonlinear coupling between the product of the diurnally varying wind and the diurnally varying conductivity .[17] The centers of the daytime vortices show a day to day variability. This can be attributed to the internal tidal modes which are sensitive to the varying meteorological conditions in the lower and in the middle atmosphere, in part also to solar activity.
Near the dip equator (where the geomagnetic field lines are horizontal), a strong band of eastward flowing currents can be observed in a range of about 150 km from the equator .[1] Such enhancement of the Sq current by a factor of about four is due to the Cowling conductivity. During a solar flare, bursts of solar radiation from the environment of an active sunspot reach the higher atmosphere, mainly at E- and D- layer heights, lasting at most for one hour. The electric conductivity increases, and the Sq current enhances on the daytime hemisphere. A small increase occurs, called geomagnetic solar flare effect or crochet.[18] During a solar eclipse, the electric conductivity decreases in the shadow region, and the Sq current and thus the Sq variation diminishes by a few nT in that area.[19] It is called a geomagnetic solar eclipse effect. Both events can be observed only during quiet geomagnetic activity.
In the aftermath of strong magnetospheric disturbances, a current system develops into a quasi anti-Sq-current. It is generated by Joule heating in the polar thermosphere.[20][21] This current system is called Ddyn.
Theory
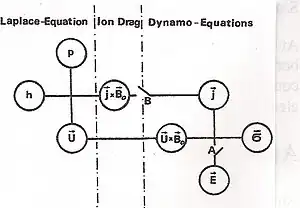
In order to determine quantitatively the dynamo action of the neutral wind U, one starts with the horizontal momentum equation of the wind together with an equation for the divergence of the wind. The momentum equation balances the inertial force, the Coriolis force, and the horizontal gradient of pressure p. In addition, the Ampere force Jx Bo couples the electric current density j to the wind and pressure system. The equivalent depth h (the eigenvalue of the tidal mode) determines the divergence of the wind. The electric current must obey Ohm's law. An electric polarization field E is generated by charge separation to enforce the condition of no sources and sinks of the current. Feedback between wind and electric current occurs via the Lorentz force Ux B. Usually, the electric conductivity tensor σ is considered as a given data set, and a height integrated conductivity tensor Σ and a height integrated sheet current J are applied.[22]
In conventional models, the Ampere force is neglected. This means that gate B in Figure 2 is open. This is called a kinematic dynamo. Models with closed gate B are called hydromagnetic dynamos. The influence of the mutual coupling between wind and current can immediately be seen if one considers an infinitely large electric conductivity σ. In the kinematic model, the electric current would become infinitely large, while the wind amplitude remains constant. In the hydromagnetic model, the current reaches an upper limit, similar to a technical dynamo during short circuit, while the wind amplitude breaks down to a fraction of its original value. Charge separation acts like a self-impedance preventing the current to become infinitely large.[17]
L-Current
Lunar (L) currents are weaker by a factor of about 20 than the Sq currents. The dominant wind component to drive these currents is the (2, 2) tidal mode. The L current is similar in shape as the Sq current, with the difference that four vortices instead of two exit. In each vortex a total current of about 4 kA flows. The seasonal variation of L is similar to that of Sq. During sunlit hours, L is strongly enhanced, while it approaches zero during the night. Thus, the L current exhibits, in addition, a modulation depending on the lunar phase.[1] The geomagnetic effect of the L-current can best been seen near the dip equator where the Cowling conductivity strongly enhances that current.[1]
DP1-Current
Interaction between solar wind plasma and the polar geomagnetic field produces a global-scale magnetospheric electric convection field directed from dawn to dusk with a potential difference of about 15 kV during quiet magnetospheric conditions, increasing substantially during disturbed conditions. Charge separation takes place at the magnetopause. This area is connected with the ionospheric dynamo region via the first open geomagnetic field lines with one footpoint within the auroral regions. Thus, electric discharging currents can flow via field-aligned currents as two small bands within the auroral zone dynamo layer, on the daytime as well as on the nighttime hemisphere. These currents are called DP1 current or auroral electrojets. Their magnitudes are of the order of Mega Amperes.[2] Ohmic losses and thus Joule heating of these currents is comparable with that due to the solar XUV heat input within middle and lower latitudes during quiet conditions and much larger during disturbed conditions. Therefore, it dominates ionospheric and thermospheric dynamics and causes ionospheric and thermospheric storms [23][24]
DP2-Current
The magnetospheric electric convection field drives a two cell current within the polar cup with their vortices situated on the morning and on the evening side. It is called DP2 current. That current exists already during quiet conditions (Sqp) and becomes enhances during disturbed conditions. It is mainly composed of electric Hall currents.[1][25]
Polar-Ring Current
If the azimuthal component of the interplanetary magnetic field (IMF) is directed toward dusk, the magnetospheric plasma is slowed down in the northern polar cap and accelerated in the southern polar cap. If the azimuthal component of the IMF is directed toward dawn, the situation is reversed. This deviation from co-rotation disappears at lower latitudes. The magnetic effect on the ground within the polar regions corresponds to an ionospheric Hall current at about 10o polar distance encircling the magnetic poles in a clockwise direction as seen by an observer standing on the ground during interplanetary sectors with fields pointing away from the Sun, and in a counterclockwise direction during toward-sector polarity [17] [26]
References
- 1 2 3 4 5 6 Chapman , S.J. and J. Bartels, „Geomagnetism“ , Clarendon Press, 1951
- 1 2 3 Akasofu, S.I., "Physics of Magnetospheric Substorms", Reidel, Dordrecht, 1977
- ↑ Heppner, J.P., in Dyer, E.R. (ed), "Critical Problems of Magnetospheric Physics", Nat. Acad. Sci.,Washington, D.C., p. 107. 1972
- ↑ Viggiano, A.A., and F. Arnold, in Volland, H. (ed), "Handbook of Atmospheric Electrodynamics", Vol. 1, p. 1, CRC Press, Boca Raton, FL, 1995
- ↑ Fejer, A.A., Rev. Geophys., 2, 275, 1964
- ↑ Longuet-Higgins, M.S., "The eigenfunctions of Laplace's tidal equations over a sphere", Phil. Trans. Roy. Soc.", London, A262, p. 511, 1968
- 1 2 Volland, H., "Atmospheric Tidal and Planetary Waves", Kluwer Publ., Dordrecht, 1988
- ↑ Günzkofer, F.; Pokhotelov, D.; Stober, G.; Liu, H.; Liu, H.-L.; Mitchell, N.J.; Tjulin, A.; Borries, C. (2022-09-25). "Determining the Origin of Tidal Oscillations in the Ionospheric Transition Region With EISCAT Radar and Global Simulation Data". Journal of Geophysical Research: Space Physics. 127 (10). doi:10.1029/2022JA030861.
- 1 2 Chapman, S., and R.S. Lindzen, "Atmospheric Tides", Kluwer Dordrecht, 1970
- ↑ Kohl, H. and J.W. King, J. Atm. Terr. Phys., 29,1045, 1967
- ↑ Fukushima, N., Radio Sci., 6, 269, 1971
- ↑ Malin, S.R.C., Phil Trans. R. Soc., London, Ser. A 274, 551,1973
- ↑ Forbes, J.M., at all., J. Geophys. Res., Space Physics, 113, 17, 2008
- ↑ Matsushita, S., and W.H. Campell, W.H. (eds.), "Physics of Geomagnetic Phenomena", Vol. I and II, Academic Press, New York,1967
- ↑ Kato, S., J. Geophys. Res., 71, 3211, 1966
- ↑ Forbes, J.M., J. Geophys.Res. 87, 5222, 1988
- 1 2 3 Volland, H., "Atmospheric Electrodynamics", Kluwer, Dordrecht, 1984
- ↑ Richmond, A.DF., and S.V. Venkatesmaran, J. Geophys. Res., 81, 139,1971
- ↑ Wagner, C.U., J. Atm. Terr. Phys., 25,529,1963
- ↑ Blanc, M., and A.D. Richmond, J. Geophys. Res., 85, 1669, 1980
- ↑ Zaka, K,.Z., et al., Ann. Geophys., 27, 3523, 2009
- ↑ Richmond, A.D., Geomagn. and Geoelectr. 31, 287,1979
- ↑ Proelss, G.W., in Volland, H. (ed), "Handbook of Atmospheric Electrodynamics", Vol. II, p.195, CRC Press, Boca Raton, FL, 1995
- ↑ Proelss, G. W., Surv. Geophys. 32, 101, 2011
- ↑ Nishida, A., and S. Kokubun, Rev. Geophys. Space Sci., 9, 417,1971
- ↑ Svalgaard, L., J. Geophys. Res., 78, 2064, 1973
Further reading
- M.C. Kelly (2009). The Earth' Ionosphere: Plasma Physics and Electrodynamics. Akademic press, New York.
- G. Proelss and M.K. Bird (2010). Physics of the Earth's Space Environment: An Introduction. Springer, Berlin.
- A. Brekke (2013). Physics of the Upper Polar Atmosphere. Springer, Berlin.
External links
 Media related to Ionospheric dynamo region at Wikimedia Commons
Media related to Ionospheric dynamo region at Wikimedia Commons