Figure 1. Fitness of individuals by density in habitat A and habitat B. According to the ideal free distribution, individuals will equalize between habitat A and habitat B so that each individual has the same fitness. According to this example, habitat A will always have more individuals than habitat B.
Figure 2. A habitat isodar for one species in two habitats. The species always prefers habitat A over habitat B. At low density, individuals will move into habitat A. As density increases, individuals will equalize fitness by dispersing to habitat B. However, habitat A will increase by double the amount as habitat B. The straight line represents equal fitness in both habitats.

Isodar is a theory of habitat selection in population biology proposed by Douglas W. Morris. The theory underscores the importance of the abundance and thus competition between the members of the same species in selecting habitats. The name "isodar" stems from "iso" in Latin meaning same and "dar" from Darwin.[1]

Background and theory

An isodar, or habitat isodar, is a theory in evolutionary ecology developed in the late 1980s by Douglas W. Morris.[2][3] Isodars model density-dependent habitat selection for one or two species in two habitats according to the ideal free and ideal despotic distributions. Isodar is a two-part word: "iso" meaning equal in Latin; "dar" for Darwinian evolution, and is defined as all combinations of population densities in habitats A and B such that both habitats offer the same fitness reward.

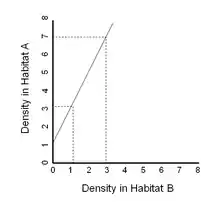
Animals displaying an ideal free distribution distribute themselves among patches (sources of a resource) in such a way that each individual get the same amount of the resource. For example, if food is twice as abundant in habitat A compared to habitat B, the ideal free distribution-based model would predict that there will accordingly be twice as many animals competing for food in habitat A compared to habitat B. If the total number of animals is considered to be variable, there are two ways this can be plotted on a two-dimensional Cartesian graph. One way is to plot two lines on a graph of fitness vs. density of individuals. This graph can be used to predict the density of individuals at any given level of fitness. The second is to plot the density of individuals in habitat A vs. the density of individuals in habitat B when the fitness of all individuals is equal. The line in this second graph is an isodar line.

Ideal free isodars predict that a species density in habitat A will increase linearly with its density in habitat B so that each individual in the species has the same fitness. If habitat A has higher quality resources than habitat B, then proportionately more individuals would be in habitat A then in habitat B. This can be shown on either a Fitness-Density graph (Figure 1) or a graph of density in two habitats (Figure 2).

Applications

Isodars can be used to study density-dependent habitat selection between two species competing for two habitats. Species will equilibrate between the two habitats two maintain equal fitness within their own species and avoid competition with the other species.[4] Isodars have also been used to show the effect of human habitat selection on biodiversity.[5] They can also be employed to examine the cost and density dependence of habitat selection in a population.[6]

Criticism leveled against the method includes the fact that in attempting to condense a very complex combination of parameters into the single metric of population density, misleading conclusions about the underlying dynamics may be suggested or supported.[7]

References

  1. ↑ Morris DW. Habitat-dependent estimates of competitive interaction. Oikos, 55, 111-120
  2. ↑ Morris, Douglas (1987). "Spatial scale and the cost of density-dependent habitat selection". Evolutionary Ecology. 1 (4): 379–388. doi:10.1007/bf02071560. S2CID 31093975.
  3. ↑ Morris, Douglas (1988). "Habitat-dependent population regulation and community structure". Evolutionary Ecology. 2 (3): 253–269. doi:10.1007/bf02214286. S2CID 514811.
  4. ↑ Morris, Douglas; D.L. Davidson; C.J. Krebs (2000). "Measuring the ghost of competition: insights from density-dependent habitat selection on the coexistence and dynamics of lemmings". Evolutionary Ecology Research. 2: 41–67.
  5. ↑ Morris, Douglas; S.R. Kingston (2002). "Predicting future threats to biodiversity from habitat selection by humans". Evolutionary Ecology Research. 4: 787–810.
  6. ↑ Lin, Y. T. K.; Batzli, G. O. (2002). "The cost of habitat selection in prairie voles: an empirical assessment using isodar analysis" (PDF). Evolutionary Ecology. 16 (4): 387–397. doi:10.1023/a:1020216502620. S2CID 43868619.
  7. ↑ Hansson, L.; Fahrig, L.; Merriam, G., eds. (1994). Mosaic landscapes and ecological processes. Vol. 2. Springer Science & Business Media.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.