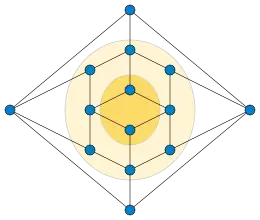
In graph theory, a k-outerplanar graph is a planar graph that has a planar embedding in which the vertices belong to at most concentric layers. The outerplanarity index of a planar graph is the minimum value of for which it is -outerplanar.
Definition
An outerplanar graph (or 1-outerplanar graph) has all of its vertices on the unbounded (outside) face of the graph. A 2-outerplanar graph is a planar graph with the property that, when the vertices on the unbounded face are removed, the remaining vertices all lie on the newly formed unbounded face. And so on.
More formally, a graph is -outerplanar if it has a planar embedding such that, for every vertex, there is an alternating sequence of at most faces and vertices of the embedding, starting with the unbounded face and ending with the vertex, in which each consecutive face and vertex are incident to each other.
Properties and applications
The -outerplanar graphs have treewidth at most .[1] However, some bounded-treewidth planar graphs such as the nested triangles graph may be -outerplanar only for very large , linear in the number of vertices.
Baker's technique covers a planar graph with a constant number of -outerplanar graphs and uses their low treewidth in order to quickly approximate several hard graph optimization problems.[2]
In connection with the GNRS conjecture on metric embedding of minor-closed graph families, the -outerplanar graphs are one of the most general classes of graphs for which the conjecture has been proved.[3]
A conjectured converse of Courcelle's theorem, according to which every graph property recognizable on graphs of bounded treewidth by finite state tree automata is definable in the monadic second-order logic of graphs, has been proven for the -outerplanar graphs.[4]
Recognition
The smallest value of for which a given graph is -outerplanar (its outerplanarity index) can be computed in quadratic time.[5]
References
- ↑ Bodlaender, Hans L. (1998), "A partial -arboretum of graphs with bounded treewidth", Theoretical Computer Science, 209 (1–2): 1–45, doi:10.1016/S0304-3975(97)00228-4, hdl:1874/18312, MR 1647486
- ↑ Baker, B. (1994), "Approximation algorithms for NP-complete problems on planar graphs", Journal of the ACM, 41 (1): 153–180, doi:10.1145/174644.174650, S2CID 9706753.
- ↑ Chekuri, Chandra; Gupta, Anupam; Newman, Ilan; Rabinovich, Yuri; Sinclair, Alistair (2006), "Embedding -outerplanar graphs into ", SIAM Journal on Discrete Mathematics, 20 (1): 119–136, doi:10.1137/S0895480102417379, MR 2257250, S2CID 13925350
- ↑ Jaffke, Lars; Bodlaender, Hans L.; Heggernes, Pinar; Telle, Jan Arne (2017), "Definability equals recognizability for -outerplanar graphs and -chordal partial -trees", European Journal of Combinatorics, 66: 191–234, doi:10.1016/j.ejc.2017.06.025, MR 3692146
- ↑ Kammer, Frank (2007), "Determining the smallest such that is -outerplanar", in Arge, Lars; Hoffmann, Michael; Welzl, Emo (eds.), Algorithms: ESA 2007, 15th Annual European Symposium, Eilat, Israel, October 8-10, 2007, Proceedings, Lecture Notes in Computer Science, vol. 4698, Springer, pp. 359–370, doi:10.1007/978-3-540-75520-3_33